Question

8B. Cho tam giác DEF vuông tại D , đường phân giác EM ( M thuộc DF ). Từ M
kẻ MN vuông góc với EF N( thuộc EF ). Giao điểm của DE và NM là O . Chứng
minh rằng:
a) EM vuông góc với DN ;
b) EM là đường phân giác của góc OEF .

nhanh giúp mình nha

Answer 1

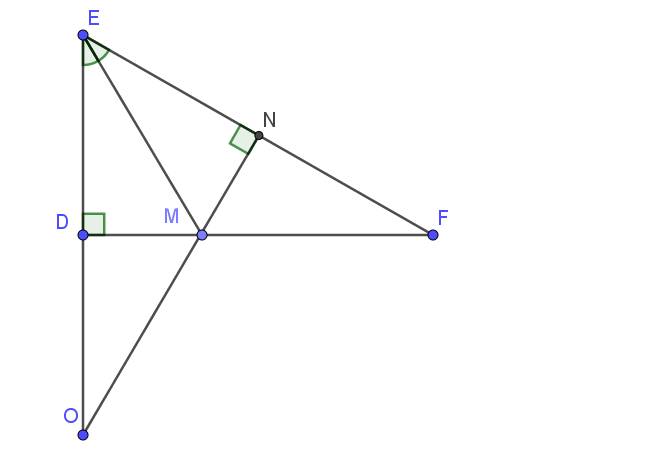
Lời giải:

a. Xét tam giác $EDM$ và $ENM$ có:

$EM$ chung

$\widehat{EDM}=\widehat{ENM}=90^0$

$\widehat{DEM}=\widehat{NEM}$ (do $EM$ là phân giác $\widehat{E}$)

$\Rightarrow \triangle EDM=\triangle ENM$ (ch-gn)

$\Rightarrow ED=EN, MD=MN$

$\Rightarrow EM$ là trung trực $DN$

$\Rightarrow EM\perp DN$

b.

$O\in DE\Rightarrow \widehat{OEF}\equiv \widehat{DEF}$

Mà $EM$ là phân giác $\widehat{DEF}$ nên $EM$ cũng là phân giác $\widehat{OEF}$

 

Answer 2

Hình vẽ: