Các câu hỏi tương tự
Tìm m để phương trình (2x + m)(x - 1) - 2x2 + mx + m - 2 = 0 có nghiệm x dương.
Dùng công thức nghiệm của phương trình bậc hai để giải các phương trình sau:
a
)
2
x
2
−
7
x
+
3
0
b
)
6
x
2
+...
Đọc tiếp
Dùng công thức nghiệm của phương trình bậc hai để giải các phương trình sau:
a ) 2 x 2 − 7 x + 3 = 0 b ) 6 x 2 + x + 5 = 0 c ) 6 x 2 + x − 5 = 0 d ) 3 x 2 + 5 x + 2 = 0 e ) y 2 − 8 y + 16 = 0 f ) 16 z 2 + 24 z + 9 = 0
Tìm nghiệm nguyên dương của PT: xy - 2x - 3y +1 = 0
Tìm nghiệm nguyên dương của phương trình:
xy2+2xy+243y+x=0
Cho đồ thị hàm số
y
2
x
2
(P) như hình vẽ. Dựa vào đồ thị, tìm m để phương trình
2
x
2
–
m
–
5
0
có hai nghiệm phân biệt. A. m −5 B. m 0 C. m 0 D. m −5
Đọc tiếp
Cho đồ thị hàm số y = 2 x 2 (P) như hình vẽ. Dựa vào đồ thị, tìm m để phương trình 2 x 2 – m – 5 = 0 có hai nghiệm phân biệt.
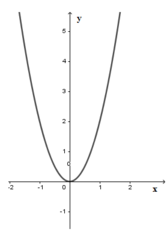
A. m < −5
B. m > 0
C. m < 0
D. m > −5
Giải hệ phương trình
2
x
2
−
y
2
+
x
y
−
5
x
+
y
+
2
y...
Đọc tiếp
Giải hệ phương trình 2 x 2 − y 2 + x y − 5 x + y + 2 = y − 2 x + 1 − 3 − 3 x x 2 − y − 1 = 4 x + y + 5 − x + 2 y − 2
Tìm các nghiệm nguyên dương của PT: xy2 + 2xy - 243y + x = 0
tìm nghiệm nguyên dương của pt : \(xy^2+2xy-243y+x=0\)
giải pt nghiệm nguyên: x2(1-y0+xy+y2=0
