Question

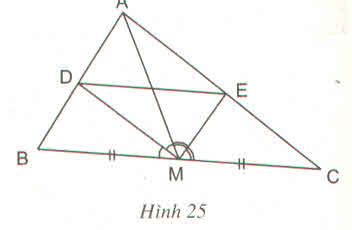
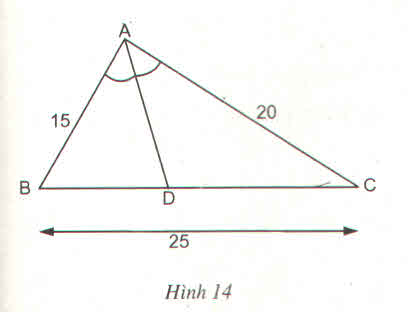
1.Tam giác ABC có độ dài các cạnh AB= m, AC= n và AD là đường phân giác. Chứng minh rẳng tỉ số diện tích tam giác ABD và diện tích tam giác ACD bằng mn. 2.Cho tam giác ABC với đường trung tuyến AM. Tia phân giác của góc AMB cắt cạnh AB ở D, tia phân giác của góc AMC cắt cạnh AC ở E. Chứng minh rằng DE // BC 3.Tam giác ABC có AB= 5cm, AC= 6cm, BC= 7cm. Tia phân giác của góc BAC cắt BC tại E. Tính các đoạn EB, EC.

Answer 1

1) AD phân giác góc A nên chia cạnh BC thành 2 đoạn tỉ lệ với 2 cạnh bên: ta có BD/DC = AB/AC
kẻ AH vuông góc BC tại H ta có S tam giác ABD = BD.AH/2 ; S tam giác ADC = DC.AH/2

VẬY S(ABD) / S(ACD) = ((BD.AH)/2) / ((CD.AH)/2) = BD/CD = AB/AC = m/n

Answer 2

mình làm nốt câu 2 vs câu 3 ở đây nha :))

Xét tam giác AMB có EM là phân giác :

\(\dfrac{EA}{EB}=\dfrac{AM}{BM}\)

Xét tam giác AMC có MD là phân giác :

\(\dfrac{AD}{DC}=\dfrac{AM}{MC}=\dfrac{AM}{BM}\) ( vì MB = MC )

\(\Rightarrow\) \(\dfrac{EA}{EB}=\dfrac{DA}{DC}\)

\(\Rightarrow\) DE // BC ( đpcm )

3) Ta có AE là đường phân giác của tam giác ABC nên ta có :

\(\dfrac{AE}{AB}=\dfrac{EC}{AC}\)

\(\)\(\dfrac{AE}{AB}=\dfrac{EC}{AC}=\dfrac{EB+EC}{AB+AC}=\dfrac{BC}{AB+AC}\)

\(\Rightarrow\) \(EB=\dfrac{AB.BC}{AB+AC}=\dfrac{5.7}{5+6}=\dfrac{35}{11}\left(cm\right)\)

\(\Rightarrow\) \(EB=BC-BE=7-\dfrac{35}{11}=\dfrac{42}{11}\left(cm\right)\)