Các câu hỏi tương tự
Cho a, b là các số thực thỏa mãn
a
0
v
à
a
≠
1
biết phương trình
a
x
-
1
a
x
2
c
o
s
(
b
x
)
có 7 nghiệm thực phân biệt. Tìm số nghiệm thực phân biệt của phương trình
a
2...
Đọc tiếp
Cho a, b là các số thực thỏa mãn a > 0 v à a ≠ 1 biết phương trình a x - 1 a x = 2 c o s ( b x ) có 7 nghiệm thực phân biệt. Tìm số nghiệm thực phân biệt của phương trình a 2 x - 2 a x ( c o s b x + 2 ) + 1 = 0
A. 14
B. 0
C. 7
D. 28
Cho đa thức H (x) = ax^2 - x + 1. Tìm a biết H(x) =có 1 nghiệm bằng 2.
Giúp mik nhanh nha nha ! Mai thi rùi =))
Cho hàm số
y
a
x
2
+
x
-
1
4
x
2
+
b
x
+
9
có đồ thị (C) trong đó a, b là các hằng số dương thỏa mãn ab 4. Biết rằng (C) có đường tiệm cận ng...
Đọc tiếp
Cho hàm số y = a x 2 + x - 1 4 x 2 + b x + 9 có đồ thị (C) trong đó a, b là các hằng số dương thỏa mãn ab = 4. Biết rằng (C) có đường tiệm cận ngang y = c và có đúng một đường tiệm cận đứng. Tính tổng T = 3 a + b - 24 c .
A. T = 11
B. T = 4
C. T = -11
D. T = 7
Cho hai đa thức
f(x)=3x2-x2+x-7+x4+6x3
g(x)= -2x2-4x4+6+4x2-6x3-x
a)Thu gọn và sắp xếp đa thức trên theo lũy thừa giảm dần của biến
b)Tính h(x)=g(x)+g(x)
c)Tìm nghiệm của đa thức h(x)
(mình cần chủ yếu là câu C)
ai trả lời gấp dùm vs sẽ có hậu tạCho hai đa thức
f(x)=3x2-x2+x-7+x4+6x3
g(x)= -2x2-4x4+6+4x2-6x3-x
a)Thu gọn và sắp xếp đa thức trên theo lũy thừa giảm dần của biến
b)Tính h(x)=g(x)+g(x)
c)Tìm nghiệm của đa thức h(x)
(mình cần chủ yếu là câu C)
Cho a, b là các số thực dương khác 1. Các hàm số
y
a
x
và
y
b
x
có đồ thị như hình vẽ bên. Đường thẳng bất kỳ song song với trục hoành và cắt đồ thị hàm số
y
a
x
,
y
b
x
, trục tung lần lượt tại M, N, A đều thỏa mãn AN 2AM. Mệnh đề nào sau đây đúng? A. b 2a B.
a...
Đọc tiếp
Cho a, b là các số thực dương khác 1. Các hàm số y = a x và y = b x có đồ thị như hình vẽ bên. Đường thẳng bất kỳ song song với trục hoành và cắt đồ thị hàm số y = a x , y = b x , trục tung lần lượt tại M, N, A đều thỏa mãn AN = 2AM. Mệnh đề nào sau đây đúng?
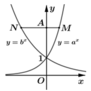
A. b = 2a
B. a 2 = b
C. a b = 1 2
D. a b 2 = 1
Cho hàm số yf(x) có đạo hàm
y
x
2
-
12
x
+
1
4
(
b
+
3
a
)
∀
x
∈
R
, biết hàm số luôn có hai cực với a, b là các số thực không âm thỏa mãn
3
b
-
a
≤
6
. Tìm giá trị lớn nhất của biểu thức P 2a+b...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm y ' = x 2 - 12 x + 1 4 ( b + 3 a ) ∀ x ∈ R , biết hàm số luôn có hai cực với a, b là các số thực không âm thỏa mãn 3 b - a ≤ 6 . Tìm giá trị lớn nhất của biểu thức P = 2a+b
A. 1
B. 9
C. 8
D. 6
Cho hàm số
y
a
x
+
b
x
−
1
có đồ thị cắt trục tung tại A(-0;1)tiếp tuyến A tại có hệ số góc -3. Khi đó giá trị a, b thỏa mãn điều kiện sau: A.
a
+
b
0
B.
a
+
b
1
C.
a
+...
Đọc tiếp
Cho hàm số y = a x + b x − 1 có đồ thị cắt trục tung tại A(-0;1)tiếp tuyến A tại có hệ số góc -3. Khi đó giá trị a, b thỏa mãn điều kiện sau:
A. a + b = 0
B. a + b = 1
C. a + b = 2
D. a + b = 3
Cho các số thực a, b, c thỏa mãn
a
+
c
b
+
1
a
+
b
+
c
+
1...
Đọc tiếp
Cho các số thực a, b, c thỏa mãn a + c > b + 1 a + b + c + 1 < 0 . Tìm số giao điểm của đồ thị hàm số y = x 3 + a x 2 + b x + c và trục Ox
A. 0
B. 2
C. 3
D. 1
