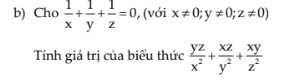\(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=0\)
\(\Rightarrow\dfrac{yz+xz+xy}{xyz}=0\)
\(\Rightarrow yz+xz+xy=0\left(x;y;z\ne0\right)\)
\(\Rightarrow a+b+c=0\left(a=yz;b=xz;c=xy\right)\left(1\right)\)
Ta có : \(A=\dfrac{yz}{x^2}+\dfrac{xz}{y^2}+\dfrac{xy}{z^2}=\dfrac{\left(yz\right)^3+\left(xz\right)^3+\left(xy\right)^3}{\left(xyz\right)^2}=\dfrac{a^3+b^3+c^3}{abc}\)
Ta lại có hệ quả của hằng đẳng thức (tự chứng minh) \(a^3+b^3+c^3-3abc=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\)
\(\Rightarrow a^3+b^3+c^3-3abc=0\) (do \(\left(1\right)\))
\(\Rightarrow a^3+b^3+c^3=3abc\)
\(\Rightarrow\dfrac{a^3+b^3+c^3}{abc}=3\)
\(\Rightarrow A=\dfrac{yz}{x^2}+\dfrac{xz}{y^2}+\dfrac{xy}{z^2}=3\)
Đúng 1
Bình luận (0)
