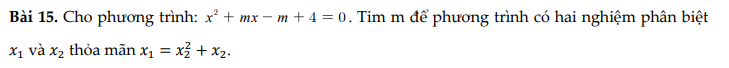a) \(x^2+mx-m+4=0\left(1\right)\)
Để \(\left(1\right)\) có \(2\) nghiệm phân biệt \(x_1;x_2\) khi và chỉ khi
\(\Leftrightarrow\Delta=m^2-4\left(4-m\right)>0\)
\(\Leftrightarrow m^2+4m-16>0\)
\(\Leftrightarrow m< -2-2\sqrt{5}\cup m>-2+2\sqrt{5}\left(2\right)\)
b) \(x_1+x_2=-m\)
mà \(x_1=x_2^2+x_2\)
\(\Rightarrow x_2^2+2x_2+m=0\left(a\right)\)
Để \(\left(a\right)\) có 2 nghiệm khi và chỉ khi
\(\Leftrightarrow\Delta'=1-m\ge0\)
\(\Leftrightarrow m\le1\) so với điều kiện \(\left(2\right)\) ta được \(m< -2-2\sqrt{5}\) thỏa mãn đề bài
Đúng 1
Bình luận (0)
