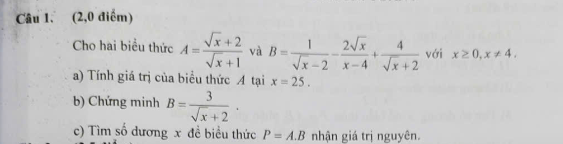a) Thay x=25 TMĐK vào A ta có:
\(A=\dfrac{\sqrt{25}+2}{\sqrt{25}+1}=\dfrac{5+2}{5+1}=\dfrac{7}{6}\)
Vậy \(A=\dfrac{7}{6}\) khi x = 25
b) Ta có: \(B=\dfrac{1}{\sqrt{x}-2}-\dfrac{2\sqrt{x}}{x-4}+\dfrac{4}{\sqrt{x}+2}\)
\(B=\dfrac{1\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{4\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}-\dfrac{2\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(B=\dfrac{\sqrt{x}+2+4\sqrt{x}-8-2\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(B=\dfrac{3\sqrt{x}-6}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\dfrac{3\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\dfrac{3}{\sqrt{x}+2}\) (đpcm)
c) \(P=A\cdot B=\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\cdot\dfrac{3}{\sqrt{x}+2}=\dfrac{3}{\sqrt{x}+1}\)
Để P nhận GT nguyên thì \(3⋮\sqrt{x}+1\Leftrightarrow\sqrt{x}+1\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
mà \(\sqrt{x}+1>0\Rightarrow\sqrt{x}+1\in\left\{1;3\right\}\Leftrightarrow x\in\left\{0;4\right\}\)
Kết hợp ĐKXĐ và x là số dương \(\Rightarrow x\in\varnothing\)
Vậy không có GT nào của x thỏa mãn đề bài