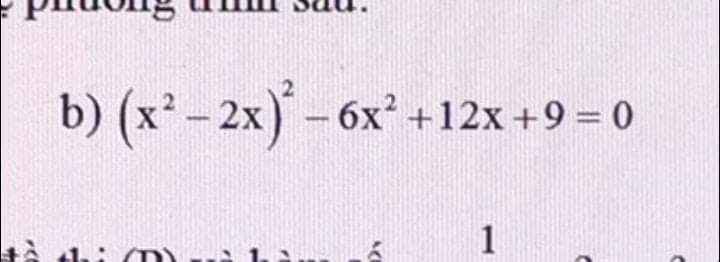\(\left(x^2-2x\right)^2-6x^2+12x+9=0\)
⇔\(\left(x^2-2x\right)^2-3\left(2x^2-4x-3\right)=0\)
⇔\(\left(x^2-2x\right)^2-3[2\left(x^2-2x\right)-3]=0\)
Đặt A=x2-2x
Ta có pt mới:\(A^2-3\left(2A-3\right)=0\)
⇔\(A^2-6A+9=0\)
⇔\(\left(A-3\right)\left(A-3\right)=0\)
⇒A-3=0
⇔A=3
⇔\(x^2-2x=3\)
⇔\(x^2-2x-3=0\)
Ta có a-b+c=1+2-3=0
Vậy phương trình có 2 nghiệm phân biệt
x1=-1
x2=\(\dfrac{3}{1}=3\)
\(\left(x^2-2x\right)^2-6x^2+12x+9=0\)
<=>\(\left(x^2-2x\right)^2-6\left(x^2-2x\right)+9=0\)
đặt \(x^2-2x=m\)
=>pt: \(m^2-6m+9=0\)
\(\Delta=\left(-6\right)^2-4.9=0\)
=> pt có nghiệm kép m1=m2=\(\dfrac{6}{2}=3\)
thay m=3 vào \(x^2-2x\) ta được \(x^2-2x=3< =>x^2-2x-3=0\)
\(\Delta1=\left(-2\right)^2-4.\left(-3\right)=16>0\)
pt có 2 nghiệm phân biệt
x1=\(\dfrac{2+\sqrt{16}}{2}=3\)
x2=\(\dfrac{2-\sqrt{16}}{2}=-1\)
vậy pt có nghiệm \(\left[{}\begin{matrix}x=3\\x=-1\end{matrix}\right.\)
Lời giải:
PT $\Leftrightarrow (x^2-2x)^2-6(x^2-2x)+9=0$
$\Leftrightarrow (x^2-2x-3)^2=0$
$\Leftrightarrow x^2-2x-3=0$
$\Leftrightarrow (x+1)(x-3)=0$
$\Rightarrow x=-1$ hoặc $x=3$