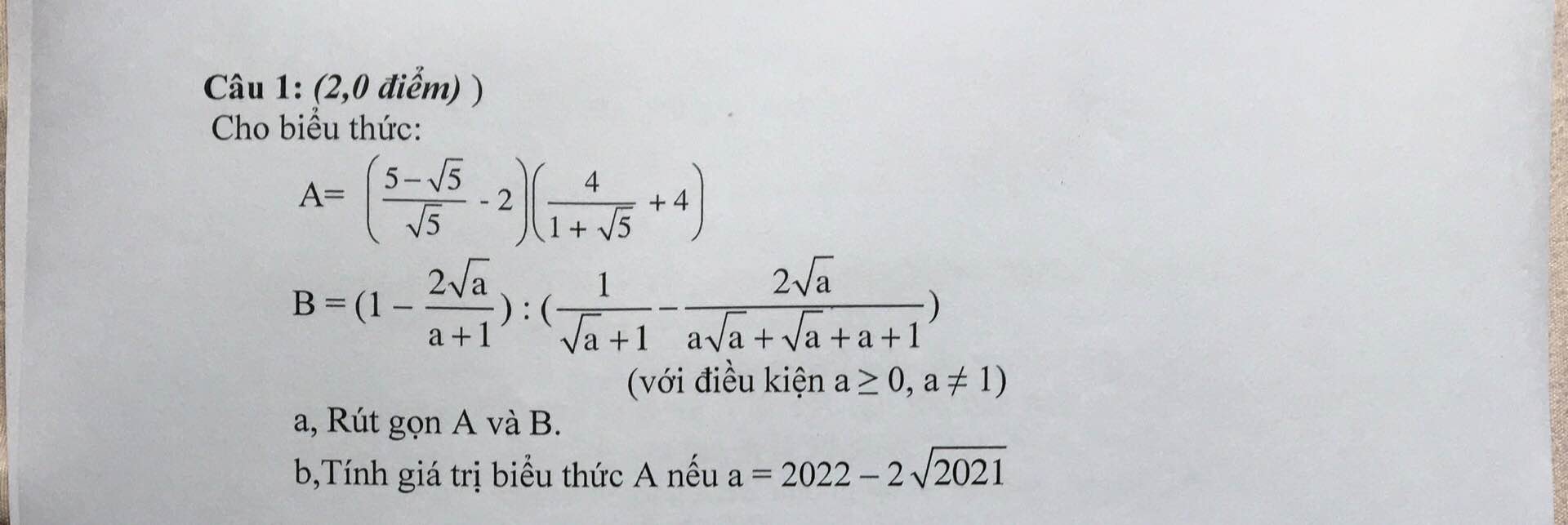\(A=\left(\dfrac{5-\sqrt{5}}{\sqrt{5}}-2\right)\left(\dfrac{4}{1+\sqrt{5}}+4\right)\)
\(=\left(\sqrt{5}-1-2\right).\left[\dfrac{4\left(\sqrt{5}-1\right)}{\left(1+\sqrt{5}\right)\left(\sqrt{5}-1\right)}+4\right]\)
\(=\left(\sqrt{5}-3\right)\left[\dfrac{4\left(\sqrt{5}-1\right)}{5-1}+4\right]\)\(=\left(\sqrt{5}-3\right)\left(\sqrt{5}-1+4\right)=\left(\sqrt{5}-3\right)\left(\sqrt{5}+3\right)=-4\)
B=\(\left(1-\dfrac{2\sqrt{a}}{a+1}\right):\left(\dfrac{1}{\sqrt{a}+1}-\dfrac{2\sqrt{a}}{a\sqrt{a}+\sqrt{a}+a+1}\right)\) ( \(a\ge0,a\ne1\))
\(=\dfrac{a+1-2\sqrt{a}}{a+1}:\left[\dfrac{1}{\sqrt{a}+1}-\dfrac{2\sqrt{a}}{\sqrt{a}\left(a+1\right)+\left(a+1\right)}\right]\)
\(=\dfrac{\left(\sqrt{a}-1\right)^2}{a+1}:\left[\dfrac{a+1}{\left(a+1\right)\left(\sqrt{a}+1\right)}-\dfrac{2\sqrt{a}}{\left(a+1\right)\left(\sqrt{a}+1\right)}\right]\)
\(=\dfrac{\left(\sqrt{a}-1\right)^2}{a+1}:\dfrac{a-2\sqrt{a}+1}{\left(a+1\right)\left(\sqrt{a}+1\right)}\)\(=\dfrac{\left(\sqrt{a}-1\right)^2}{a+1}.\dfrac{\left(a+1\right)\left(\sqrt{a}+1\right)}{\left(\sqrt{a}-1\right)^2}\)
\(=\sqrt{a}+1\)
b, \(B=\sqrt{a}+1=\sqrt{2022-2\sqrt{2021}}+1\)\(=\sqrt{2021-2\sqrt{2021}+1}+1\)
\(=\sqrt{\left(\sqrt{2021}-1\right)^2}+1=\)\(\left|\sqrt{2021}-1\right|+1\)\(=\sqrt{2021}-1+1=\sqrt{2021}\)