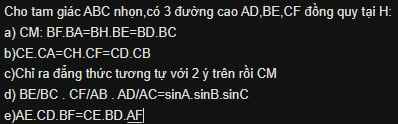
a) Xét các tam giác vuông \(\text{BHF}\) và \(\text{BEA}\), ta có:
\(\widehat{B}\) là góc chung
\(\widehat{\text{BHF}}=\widehat{\text{BEA}}=90^o\) (đường cao)
\(\Rightarrow\Delta BHF\sim\Delta BEA\left(g.g\right)\)
\(\Rightarrow\dfrac{BF}{BE}=\dfrac{BH}{BA}\)
\(\Rightarrow BF.BA=BE.BH\left(1\right)\)
Xét các tam giác vuông \(\text{BHC}\) và \(\text{BDA}\), ta có:
\(\widehat{B}\) là góc chung
\(\widehat{\text{BHC}}=\widehat{\text{BDA}}=90^o\) (đường cao)
\(\Rightarrow\Delta BHC\sim\Delta BDA\left(g.g\right)\)
\(\Rightarrow\dfrac{BH}{BD}=\dfrac{BC}{BA}\)
\(\Rightarrow BH.BA=BD.BC\left(2\right)\)
\(\left(1\right);\left(2\right)\Rightarrow BF.BA=BH.BE=BD.BC\left(đpcm\right)\)
b) Chứng minh tương tự như câu a), ta sẽ được:
\(\Delta CHF\sim\Delta CEA\Rightarrow CH.CF=CE.CA\)
\(\Delta CHD\sim\Delta CBA\Rightarrow CD.CB=CE.CA\)
\(\Rightarrow\text{CE.CA = CH.CF = CD.CB}\left(đpcm\right)\)
c) Các đẳng thức tương tự đã được chứng minh ở câu a) và b)
\(AF.AC=AH.AD=CD.CB\)
d) Từ các cặp tam giác đồng dạng trên ta có :
\(\dfrac{BE}{BC}=sinC\)
\(\dfrac{CF}{AB}=sinB\)
\(\dfrac{AD}{AC}=sinA\)
\(\Rightarrow\dfrac{BE}{BC}.\dfrac{CF}{AB}.\dfrac{AD}{AC}=sinC.sinB.sinA=sinA.sinB.sinC\left(đpcm\right)\)