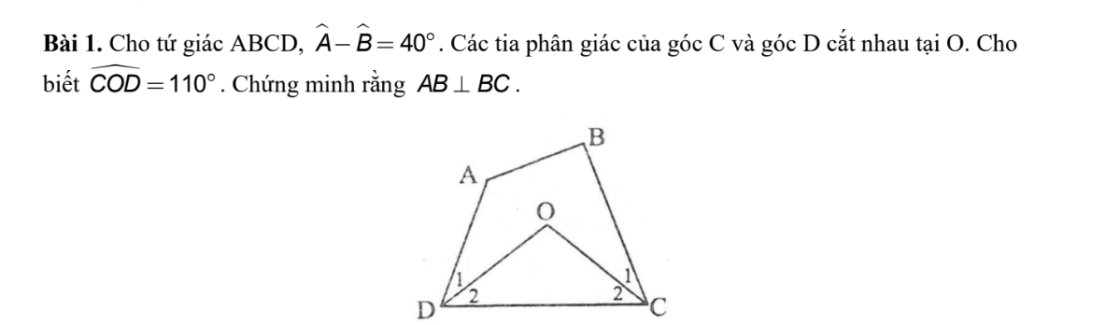
Xét \(\Delta OCD\) có \(\widehat{COD}+\widehat{OCD}+\widehat{ODC}=180^o\Rightarrow\widehat{OCD}+\widehat{ODC}=180^o-\widehat{COD}=180^o-110^o=70^o\)
CO, DO lần lượt là phân giác của \(\widehat{BCD},\widehat{ADC}\) nên \(\widehat{BCD}=2\widehat{OCD},\widehat{ADC}=2\widehat{ODC}\Rightarrow\widehat{BCD}+\widehat{ADC}=2\left(\widehat{OCD}+\widehat{ODC}\right)=2.70^o=140^o\)
Xét tứ giác ABCD có \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\Rightarrow\widehat{A}+\widehat{B}=360^o-\left(\widehat{C}+\widehat{D}\right)=360^o-140^o=220^o\Rightarrow\widehat{A}=220^o-\widehat{B}\)
\(\widehat{A}-\widehat{B}=40^o\Rightarrow\left(220^o-\widehat{B}\right)-\widehat{B}=40^o\Rightarrow220^o-2\widehat{B}=40^o\Rightarrow2\widehat{B}=180^o\Rightarrow\widehat{B}=90^o\)
Do đó \(AB\perp CD\)