Question

Answer 1

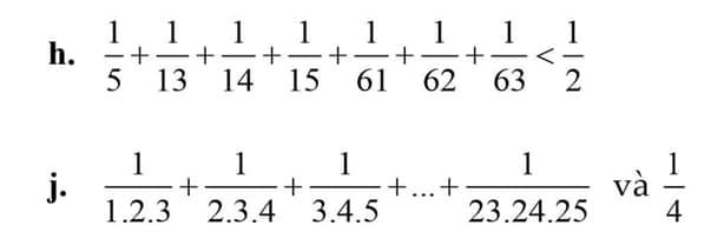
j.

Đặt $A=\frac{1}{1.2.3}+\frac{1}{2.3.4}+\frac{1}{3.4.5}+....+\frac{1}{23.24.25}$

$2A=\frac{2}{1.2.3}+\frac{2}{2.3.4}+\frac{2}{3.4.5}+....+\frac{2}{23.24.25}$

$=\frac{3-1}{1.2.3}+\frac{4-2}{2.3.4}+\frac{5-3}{3.4.5}+....+\frac{25-23}{23.24.25}$

$=\frac{1}{1.2}-\frac{1}{2.3}+\frac{1}{2.3}-\frac{1}{3.4}+\frac{1}{3.4}-\frac{1}{4.5}+...+\frac{1}{23.24}-\frac{1}{24.25}$

$=\frac{1}{2}-\frac{1}{24.25}< \frac{1}{2}$

$\Rightarrow A< \frac{1}{4}$

 

Answer 2

h/

$\frac{1}{5}+\frac{1}{13}+\frac{1}{14}+\frac{1}{15}+\frac{1}{61}+\frac{1}{62}+\frac{1}{63}$

$< \frac{1}{5}+\frac{3}{12}+\frac{3}{60}=\frac{1}{2}$