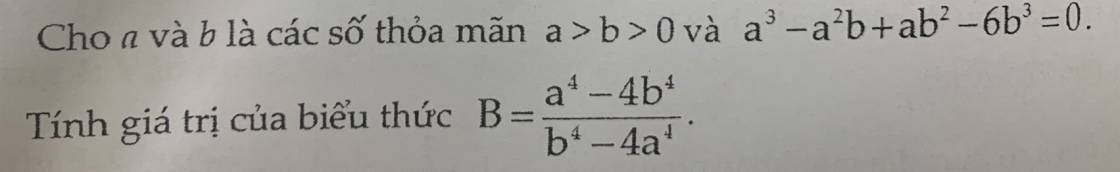Với \(a>b>0\), ta có:
\(a^3-a^2b+ab^2-6b^3=0\\\Leftrightarrow a^3-2a^2b+a^2b-2ab^2+3ab^2-6b^3=0\\\Leftrightarrow a^2(a-2b)+ab(a-2b)+3b^2(a-2b)=0\\\Leftrightarrow(a-2b)(a^2+ab+3b^2)=0\\\Leftrightarrow a-2b=0 (\text{vì } a^2+ab+3b^2>0\forall a,b>0)\\\Leftrightarrow a=2b(\text{tmđk } a>b)\)
Khi đó: \(B=\dfrac{a^4-4b^4}{b^4-4a^4}=\dfrac{(2b)^4-4b^4}{b^4-4.(2a)^4}=\dfrac{12b^4}{-63b^4}=-\dfrac{4}{21}\)
$\text{#}Toru$
Đúng 1
Bình luận (0)
