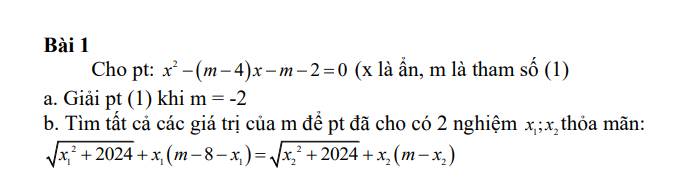Lời giải:
a.
Khi $m=-2$ thì PT trở thành:
$x^2+6x=0$
$\Leftrightarrow x(x+6)=0$
$\Leftrightarrow x=0$ hoặc $x+6=0$
$\Leftrightarrow x=0$ hoặc $x=-6$
b.
$\Delta=(m-4)^2+4(m+2)=m^2-4m+24=(m-2)^2+20>0$ với mọi $m\in\mathbb{R}$
$\Rightarrow$ PT (1) luôn có 2 nghiệm $x_1,x_2$ phân biệt với mọi $m$.
Áp dụng định lý Viet:
$x_1+x_2=m-4$
$x_1x_2=-(m+2)$
$\Rightarrow m-x_2=x_1+4; m-x_1=x_2+4$
Khi đó:
$\sqrt{x_1^2+2024}+x_1(m-8-x_1)=\sqrt{x_2^2+2024}+x_2(m-x_2)$
$\Leftrightarrow \sqrt{x_1^2+2024}-\sqrt{x_2^2+2024}+x_1(x_2+4-8)-x_2(x_1+4)=0$
$\Leftrightarrow \frac{x_1^2-x_2^2}{\sqrt{x_1^2+2024}+\sqrt{x_2^2+2024}}-4(x_1+x_2)=0$
$\Leftrightarrow (x_1+x_2)[\frac{x_1-x_2}{\sqrt{x_1^2+2024}+\sqrt{x_2^2+2024}}-4]=0$
$\Leftrightarrow x_1+x_2=0$ hoặc $\frac{x_1-x_2}{\sqrt{x_1^2+2024}+\sqrt{x_2^2+2024}}=4$
Với $x_1+x_2=0\Leftrightarrow m-4=0\Leftrightarrow m=4$
Với $\frac{x_1-x_2}{\sqrt{x_1^2+2024}+\sqrt{x_2^2+2024}}=4$:
Ta thấy:
Khi $x_1\leq x_2$ thì hiển nhiên điều trên vô lý
Khi $x_1> x_2$:
$\sqrt{x_1^2+2024}+\sqrt{x_2^2+2024}> \sqrt{x_1^2}+\sqrt{x_2^2}=|x_1|+|x_2|\geq x_1-x_2$
$\Rightarrow \frac{x_1-x_2}{\sqrt{x_1^2+2024}+\sqrt{x_2^2+2024}}< \frac{x_1-x_2}{x_1-x_2}=1< 4$ (loại)
Vậy $m=4$