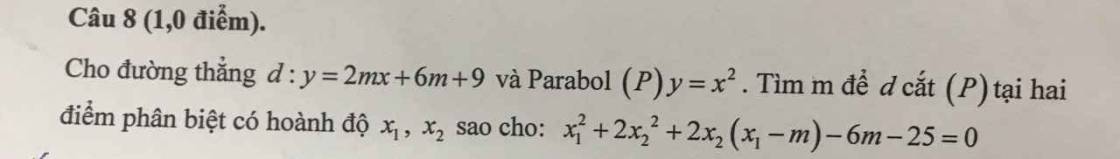Xét PT hoành độ giao điểm (P) và (d) có:
\(x^2=2mx+6m+9\Leftrightarrow x^2-2mx-6m-9=0\) (1)
\(\Delta'=\left(-m\right)^2-1\cdot\left(-6m-9\right)=m^2+6m+9=\left(m+3\right)^2\)
Để (d) cắt (P) tại 2 điểm phân biệt thì PT(1) có 2 nghiệm pb
\(\Leftrightarrow\Delta'>0\Leftrightarrow\left(m+3\right)^2>0\Leftrightarrow m\ne-3\)
Theo Vi-ét ta có: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=-6m-9\end{matrix}\right.\)
Theo đề bài có: \(x_1^2+2x_2^2+2x_2\left(x_1-m\right)-6m-25=0\)
\(\Leftrightarrow x_1^2++2x_1x_2+x_2^2+x_2^2-2mx_2-6m-9-16=0\)
\(\Leftrightarrow x_1^2+2x_1x_2+2x_2^2-\left(x_1+x_2\right)x_2+x_1x_2-16=0\)
\(\Leftrightarrow x_1^2+2x_1x_2+2x_2^2-x_1x_2-x_2^2+x_1x_2-16=0\)
\(\Leftrightarrow x_1^2+2x_1x_2+x_2^2=16\)
\(\Leftrightarrow\left(x_1+x_2\right)^2=16\)
\(\Leftrightarrow\left(2m\right)^2=16\)
\(\Leftrightarrow\left[{}\begin{matrix}2m=4\\2m=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=2\\m=-2\end{matrix}\right.\)(T/m)
Vậy m = \(\left\{2;-2\right\}\) là GT cần tìm