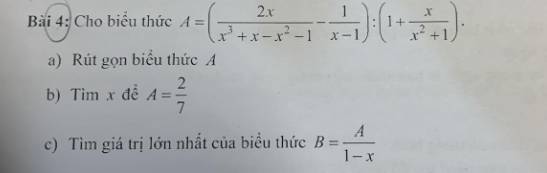Lời giải:
a. ĐKXĐ: $x\neq 1$
\(A=\left[\frac{2x}{x^2(x-1)+(x-1)}-\frac{1}{x-1}\right]:\frac{x^2+x+1}{x^2+1}\\ =\left[ \frac{2x}{(x-1)(x^2+1)}-\frac{x^2+1}{(x^2+1)(x-1)} \right].\frac{x^2+1}{x^2+x+1}\\ =\frac{2x-(x^2+1)}{(x-1)(x^2+1)}.\frac{x^2+1}{x^2+x+1}\\ =\frac{-(x-1)^2(x^2+1)}{(x-1)(x^2+1)(x^2+x+1)}=\frac{1-x}{x^2+x+1}\)
b.
\(A=\frac{1-x}{x^2+x+1}=\frac{2}{7}\\ \Leftrightarrow 7(1-x)=2(x^2+x+1)\\ \Leftrightarrow 2x^2+2x+2+7x-7=0\\ \Leftrightarrow 2x^2+9x-5=0\\ \Leftrightarrow (2x-1)(x+5)=0\)
$\Leftrightarrow 2x-1=0$ hoặc $x+5=0$
$\Leftrightarrow x=\frac{1}{2}$ hoặc $x=-5$ (tm)
c.
\(B=\frac{A}{1-x}=\frac{1-x}{x^2+x+1}:(1-x)=\frac{1}{x^2+x+1}\)
Với $x\neq 1$ thì $x^2+x+1=(x+\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
$\Rightarrow B\leq 1: \frac{3}{4}=\frac{4}{3}$
Vậy $B_{\max}=\frac{4}{3}$. Giá trị này đạt tại $x+\frac{1}{2}=0\Leftrightarrow x=\frac{-1}{2}$