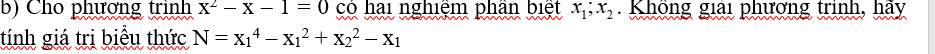Lời giải:
Áp dụng định lý Viet:
$x_1+x_2=1$
$x_1x_2=-1$
Khi đó:
$N=x_1^4-x_1^2+x_2^2-x_1=x_1^2(x_1^2-1)+x_2^2-x_1$
$=x_1^2[x_1^2-(x_1+x_2)^2]+x_2^2-x_1$
$=-x_1^2(x_2^2+2x_1x_2)+x_2^2-x_1$
$=-(x_1x_2)^2-2x_1^2(x_1x_2)+x_2^2-x_1$
$=-1+2x_1^2+x_2^2-x_1$
$=-1+2x_1^2+x_2^2-x_1(x_1+x_2)=-1+x_1^2+x_2^2-x_1x_2$
$=-1+(x_1+x_2)^2-2x_1x_2-x_1x_2=-1+(x_1+x_2)^2-3x_1x_2$
$=-1+1^2-3(-1)=-1+1+3=3$
Đúng 1
Bình luận (0)
