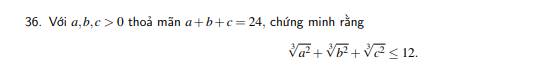Lời giải:
Áp dụng BĐT AM-GM:
$a+a+8\geq 3\sqrt[3]{8a^2}=6\sqrt[3]{a^2}$
$b+b+8\geq 6\sqrt[3]{b^2}$
$c+c+8\geq 6\sqrt[3]{c^2}$
Cộng theo vế 3 BĐT trên và thu gọn ta được:
$\sqrt[3]{a^2}+\sqrt[3]{b^2}+\sqrt[3]{c^2}\leq \frac{2(a+b+c)+24}{6}=\frac{2.24+24}{6}=12$
Ta có đpcm
Dấu "=" xảy ra khi $a=b=c=8$
Đúng 1
Bình luận (0)