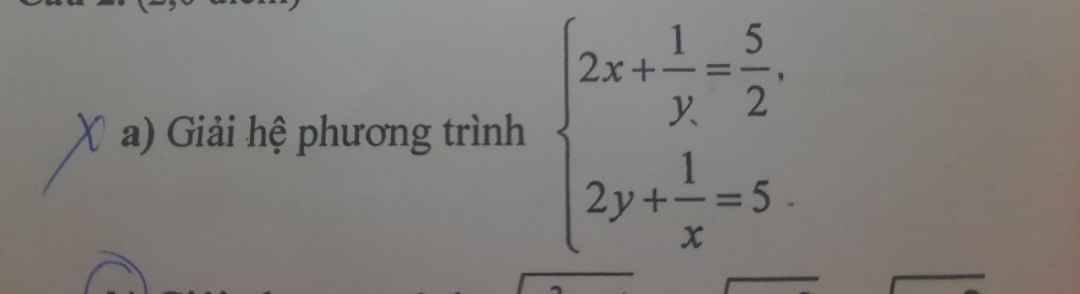Gọi `1/y` là `y` và `1/x` là `x` ta có hpt
\(\left\{{}\begin{matrix}2x+y=\dfrac{5}{2}\\2y+x=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x+y=\dfrac{5}{2}\\x+2y=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x+y=\dfrac{5}{2}\\2x+4y=10\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}-3y=-\dfrac{15}{2}\\2x+4y=10\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{5}{2}\\2x+4\cdot\dfrac{5}{2}=10\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{5}{2}\\2x=0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{5}{2}\\x=0\end{matrix}\right.\)
Thay `1/y` và `1/x` vào hpt ta có :
\(\left\{{}\begin{matrix}\dfrac{1}{y}=\dfrac{5}{2}\\\dfrac{1}{x}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{2}{5}\\x=0\end{matrix}\right.\)
Vậy hpt có một nghiệm duy nhất `(x,y)=(0;2/5)`