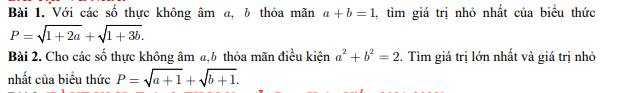Question

Answer 1

Bài 1:

$P^2=1+2a+1+3b+2\sqrt{(1+2a)(1+3b)}$

$=2+2(a+b)+b+2\sqrt{(1+2a)(1+3b)}=4+b+2\sqrt{(1+2a)(1+3b)}

$=4+b+2\sqrt{(3a+b)(a+4b)}$

$\geq 4+b+2\sqrt{(\sqrt{3}a+2b)^2}$ (áp dụng BĐT Bunhiacopxky)

$=4+b+2(\sqrt{3}a+2b)$

$=4+2\sqrt{3}(a+b)+(5-2\sqrt{3})b\geq 4+2\sqrt{3}(a+b)=4+2\sqrt{3}$

$\Rightarrow P\geq \sqrt{3}+1$
Vậy $P_{\min}=\sqrt{3}+1$
Giá trị này đạt tại $(a,b)=(1,0)$

Answer 2

Bài 2:

Tìm max:
Áp dụng BĐT Bunhiacopxky và AM-GM:
$P^2=(\sqrt{a+1}+\sqrt{b+1})^2\leq (a+1+b+1)(1+1)=2(a+b+2)$

$\leq 2[\sqrt{2(a^2+b^2)}+2]=2(\sqrt{2.2}+2)=8$

$\Rightarrow P\leq 2\sqrt{2}$

Vậy $P_{\max}=2\sqrt{2}$ khi $(a,b)=(1,1)$

----------------------------------------------------------
Tìm min:

$a^2+b^2=2\Rightarrow a\leq \sqrt{2}, b\leq \sqrt{2}$

$\Rightarrow 1\geq \frac{a}{\sqrt{2}}, 1\geq \frac{b}{\sqrt{2}}$

$P^2=a+b+2+2\sqrt{(a+1)(b+1)}=a+b+2+2\sqrt{ab+a+b+1}$

$\geq a+b+2+2\sqrt{a+b+1}$
Đặt $\sqrt{a+b+1}=t(t\geq 0)$ thì $P^2\geq t^2+1+2t=(t+1)^2$

$\Rightarrow P\geq t+1$

Có:

$t^2=a+b+1\geq a.\frac{a}{\sqrt{2}}+b.\frac{b}{\sqrt{2}}+1=\frac{1}{\sqrt{2}}(a^2+b^2)+1=\frac{1}{\sqrt{2}}.2+1=\sqrt{2}+1$

$\Rightarrow t\geq \sqrt{1+\sqrt{2}}$

$\Rightarrow P\geq t+1\geq 1+\sqrt{\sqrt{2}+1}$

Vậy $P_{\min}=1+\sqrt{\sqrt{2}+1}$

Giá trị này đạt tại $(a,b)=(\sqrt{2},0)$ và hoán vị.