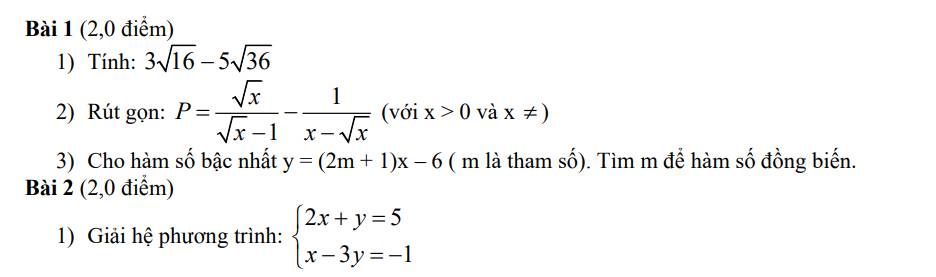Bài 1 :
1) \(3\sqrt[]{16}-5\sqrt[]{36}\)
\(=3.4-5.6\)
\(=12-30=-18\)
2) \(P=\dfrac{\sqrt[]{x}}{\sqrt[]{x}-1}-\dfrac{1}{x-\sqrt[]{x}}\left(x>0;x\ne1\right)\)
\(\Leftrightarrow P=\dfrac{\sqrt[]{x}}{\sqrt[]{x}-1}-\dfrac{1}{\sqrt[]{x}\left(\sqrt[]{x}-1\right)}\)
\(\Leftrightarrow P=\dfrac{x-1}{\sqrt[]{x}\left(\sqrt[]{x}-1\right)}\)
\(\Leftrightarrow P=\dfrac{\left(\sqrt[]{x}-1\right)\left(\sqrt[]{x}+1\right)}{\sqrt[]{x}\left(\sqrt[]{x}-1\right)}\)
\(\Leftrightarrow P=\dfrac{\sqrt[]{x}+1}{\sqrt[]{x}}=1+\dfrac{1}{\sqrt[]{x}}\)
3) \(y=\left(2m+1\right)x-6\)
Để hàm số trên đồng biến
\(\Leftrightarrow2m+1>0\)
\(\Leftrightarrow m>-\dfrac{1}{2}\)
Bài 2 :
\(\left\{{}\begin{matrix}2x+y=5\\x-3y=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}6x+3y=15\\x-3y=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}7x=14\\2x+y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=5-2x=5-2.2=1\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)