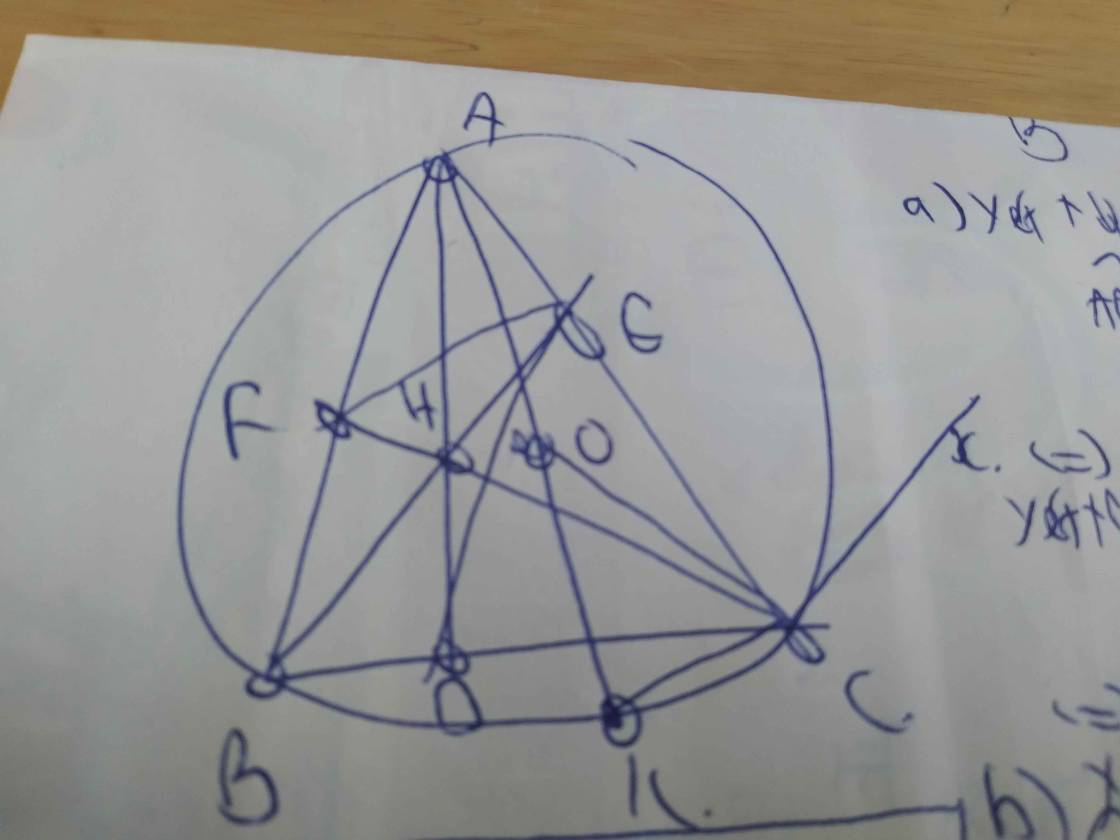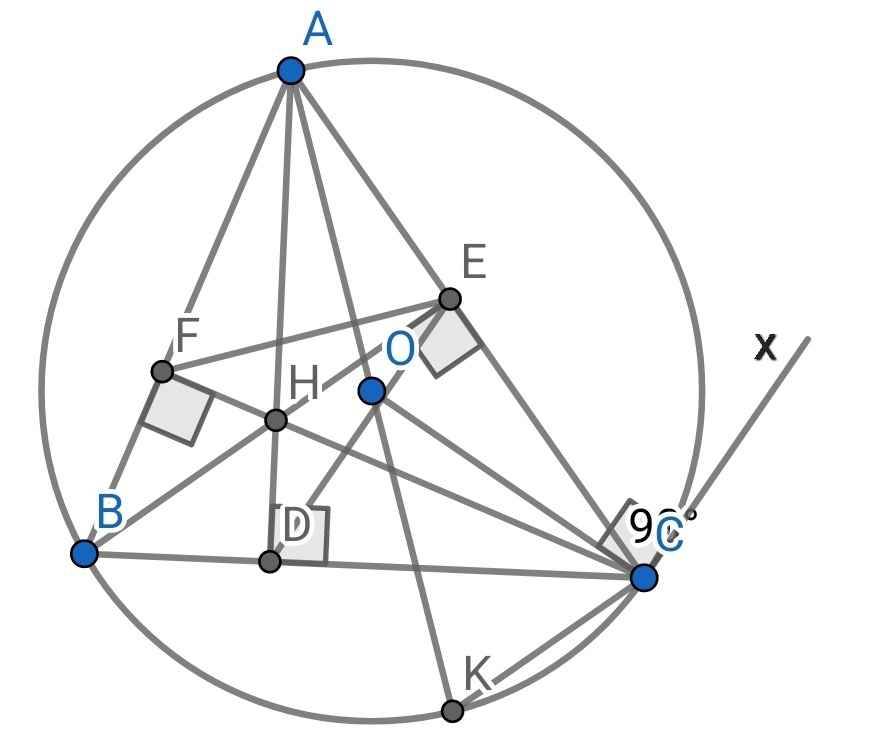
a) *) Xét tứ giác AEHF có:
∠AEH = ∠AFH = 90⁰
⇒ ∠AEH + ∠AFH = 90⁰ + 90⁰ = 180⁰
⇒ AEHF nội tiếp
*) Xét tứ giác BFEC có:
BEC = BFC = 90⁰
⇒ E, F cùng nhìn cạnh BC dưới một góc 90⁰
⇒ BFEC nội tiếp
b) Ta có:
AK là đường kính của (O) (gt)
⇒ ∠ACK = 90⁰ (góc nội tiếp chắn nửa đường tròn)
Xét hai tam giác vuông: ∆ABD và ∆AKC có:
∠ABD = ∠AKC (hai góc nội tiếp cùng chắn cung AC của (O))
⇒ ∆ABD ∽ ∆AKC (g-g)
⇒ AB/AK = AD/AC
⇒ AB.AC = AK.AD
c) Xét tứ giác ABDE có:
∠ADB = ∠AEB = 90⁰
⇒ D, E cùng nhìn AB dưới một góc 90⁰
⇒ ABDE nội tiếp
⇒ ∠BAD = ∠BED (hai góc nội tiếp cùng chắn cung AD)
Mà ∠BAD + ∠ABC = 90⁰
⇒ ∠BED + ∠ABC = 90⁰
Lại có:
∠BED + ∠CED = 90⁰
⇒ ∠CED = ∠ABC
Vẽ tia Cx là tiếp tuyến tại C của (O)
Ta có:
∠ABC = ∠ACx (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung AC cùng chắn cung AC)
Mà ∠ABC = ∠CED (cmt)
⇒ ∠ACx = ∠CED
Mà ∠ACx và ∠CED là hai góc so le trong
⇒ Cx // DE
Mà Cx ⊥ OC (do Cx là tiếp tuyến tại C của (O))
⇒ OC ⊥ DE