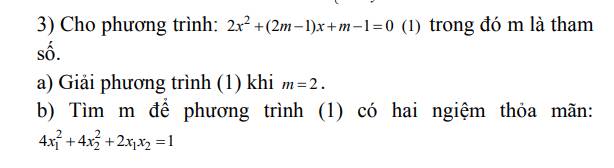Lời giải:
a. Khi $m=2$ thì pt trở thành:
$2x^2+3x+1=0$
$\Leftrightarrow (x+1)(2x+1)=0$
$\Leftrightarrow x+1=0$ hoặc $2x+1=0$
$\Leftrightarrow x=-1$ hoặc $x=\frac{-1}{2}$
b.
Để pt có 2 nghiệm thì $\Delta=(2m-1)^2-8(m-1)\geq 0$
$\Leftrightarrow 4m^2-4m+1-8m+8\geq 0$
$\Leftrightarrow 4m^2-12m+9\geq 0$
$\Leftrightarrow (2m-3)^2\geq 0\Leftrightarrow m\in\mathbb{R}$
Áp dụng định lý Viet, với $x_1, x_2$ là nghiệm của pt thì:
$x_1+x_2=\frac{1-2m}{2}; x_1x_2=\frac{m-1}{2}$
Khi đó:
$4x_1^2+4x_2^2+2x_1x_2=1$
$\Leftrightarrow 4(x_1^2+x_2^2+2x_1x_2)-6x_1x_2=1$
$\Leftrightarrow 4(x_1+x_2)^2-6x_1x_2=1$
$\Leftrightarrow (1-2m)^2-3(m-1)=1$
$\Leftrightarrow 4m^2-4m+1-3m+3=1$
$\Leftrightarrow 4m^2-7m+3=0$
$\Leftrightarrow (m-1)(4m-3)=0$
$\Leftrightarrow m=1$ hoặc $m=\frac{3}{4}$ (tm)