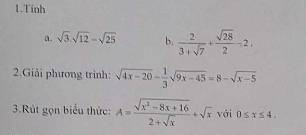Bài 1:
a.
\(\sqrt{3}.\sqrt{12}-\sqrt{25}=\sqrt{36}-\sqrt{25}=6-5=1\)
b.
\(=\frac{2(3-\sqrt{7})}{(3+\sqrt{7})(3-\sqrt{7})}+\frac{2\sqrt{7}}{2}-2\\ =\frac{2(3-\sqrt{7})}{2}+\sqrt{7}-2=3-\sqrt{7}+\sqrt{7}-2=1\)
2.
ĐKXĐ: $x\geq 5$
PT \(\Leftrightarrow \sqrt{4(x-5)}-\frac{1}{3}\sqrt{9(x-5)}=8-\sqrt{x-5}\)
\(\Leftrightarrow 2\sqrt{x-5}-\frac{1}{3}.3\sqrt{x-5}=8-\sqrt{x-5}\\ \Leftrightarrow \sqrt{x-5}=8-\sqrt{x-5}\\ \Leftrightarrow 2\sqrt{x-5}=8\\ \Leftrightarrow \sqrt{x-5}=4\\ \Leftrightarrow x-5=4^2=16\\ \Leftrightarrow x=16+5=21(\text{thỏa mãn})\)
Bài 3:
\(A=\frac{\sqrt{x^2-8x+16}}{2+\sqrt{x}}+\sqrt{x}=\frac{\sqrt{(x-4)^2}}{2+\sqrt{x}}+\sqrt{x}\)
\(=\frac{|x-4|}{\sqrt{x}+2}+\sqrt{x}=\frac{|(\sqrt{x}-2)(\sqrt{x}+2)}{\sqrt{x}+2}+\sqrt{x}\\ =\frac{|\sqrt{x}-2|(\sqrt{x}+2)}{\sqrt{x}+2}+\sqrt{x}\\ =|\sqrt{x}-2|+\sqrt{x}\)
Vì $0\leq x\leq 4$ nên $\sqrt{x}-2\leq 0$
$\Rightarrow A=2-\sqrt{x}+\sqrt{x}=2$