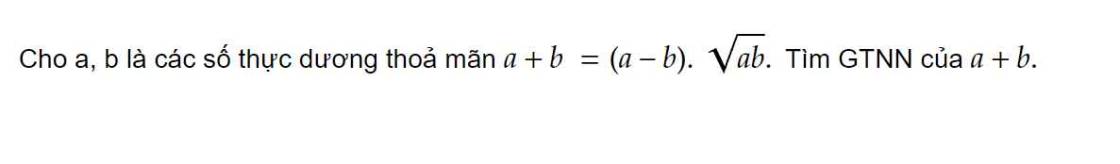Question

Answer 1

\(a,b>0\). \(a+b=\left(a-b\right)\sqrt{ab}\left(1\right)\) \(\Rightarrow a>b;ab>1\)

\(\left(1\right)\Rightarrow\left(a+b\right)^2=\left(a-b\right)^2ab\)

\(\Leftrightarrow\left(a+b\right)^2=\left[\left(a+b\right)^2-4ab\right]ab\)

\(\Leftrightarrow\left(a+b\right)^2=\left(a+b\right)^2ab-4a^2b^2\)

\(\Leftrightarrow4a^2b^2=\left(a+b\right)^2\left(ab-1\right)\)

\(\Leftrightarrow\left(a+b\right)^2=\dfrac{4a^2b^2}{ab-1}\)

Áp dụng bất đẳng thức Cauchy, ta có:

\(\dfrac{4a^2b^2}{\left(ab-1\right).1}\ge\dfrac{4a^2b^2}{\dfrac{\left[\left(ab-1\right)+1\right]^2}{4}}=16\)

\(\Rightarrow\left(a+b\right)^2\ge16\Rightarrow a+b\ge4\)

Đẳng thức xảy ra khi \(\left\{{}\begin{matrix}ab=2\\a+b=\left(a-b\right)\sqrt{2}\end{matrix}\right.;a,b>0;a>b\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{\sqrt{2}}{\sqrt{2}-1}\\b=\dfrac{\sqrt{2}}{\sqrt{2}+1}\end{matrix}\right.\)

Vậy \(Min\left(a+b\right)=4\)