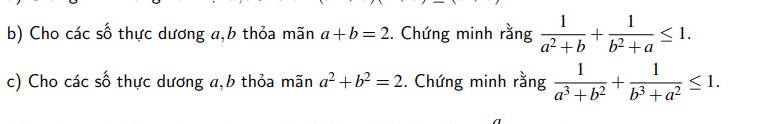a) \(a,b>0;a+b=2\)
Áp dụng bất đẳng thức Cauchy-Schwartz, ta có:
\(\dfrac{1}{a^2+b}+\dfrac{1}{b^2+a}=\dfrac{1+b}{\left(a^2+b\right)\left(1+b\right)}+\dfrac{1+a}{\left(b^2+a\right)\left(1+a\right)}\le\dfrac{1+b}{\left(a+b\right)^2}+\dfrac{1+a}{\left(a+b\right)^2}=\dfrac{2+2}{2^2}=1\left(đpcm\right)\)
Đẳng thức xảy ra khi \(a=b=1\)
b) \(a,b>0;a^2+b^2=2\)
Áp dụng bất đẳng thức Cauchy-Schwartz, ta có:
\(\dfrac{1}{a^3+b^2}+\dfrac{1}{b^3+a^2}=\dfrac{a+b^2}{\left(a^3+b^2\right)\left(a+b^2\right)}+\dfrac{b+a^2}{\left(b^3+a^2\right)\left(b+a^2\right)}\le\dfrac{a+b+a^2+b^2}{\left(a^2+b^2\right)^2}=\dfrac{a+b+2}{4}\le\dfrac{\sqrt{2\left(a^2+b^2\right)}+2}{4}=1\left(đpcm\right)\)
Đẳng thức xảy ra khi \(a=b=1\)
b)Ta có:
\(\dfrac{1}{a^2-a+2}\le\dfrac{3}{4}-\dfrac{1}{4}a\left(\text{*}\right)\) với mọi \(a\) thoả mãn \(0< a< 2\)
Thật vậy, BĐT \(\left(\text{*}\right)\) tương đương với:
\(4\le\left(3-a\right)\left(a^2-a+2\right)\Leftrightarrow a^3-4a^2+5a-2\le0\)
\(\Leftrightarrow\left(a-2\right)\left(a-1\right)^2\le0\), đúng với mọi \(a\) thoả mãn \(0< a< 2\)
Ta có: với \(a,b\) là các số thực dương thoả mãn \(a+b=2\) thì \(0< a,b< 2\)
Áp dụng BĐT \(\left(\text{*}\right)\), ta có:
\(VT=\dfrac{1}{a^2-a+2}+\dfrac{1}{b^2-b+2}\le\dfrac{3}{2}-\dfrac{1}{4}\left(a+b\right)=1\)
Đẳng thức xảy ra khi và chỉ khi \(a=b=1\)