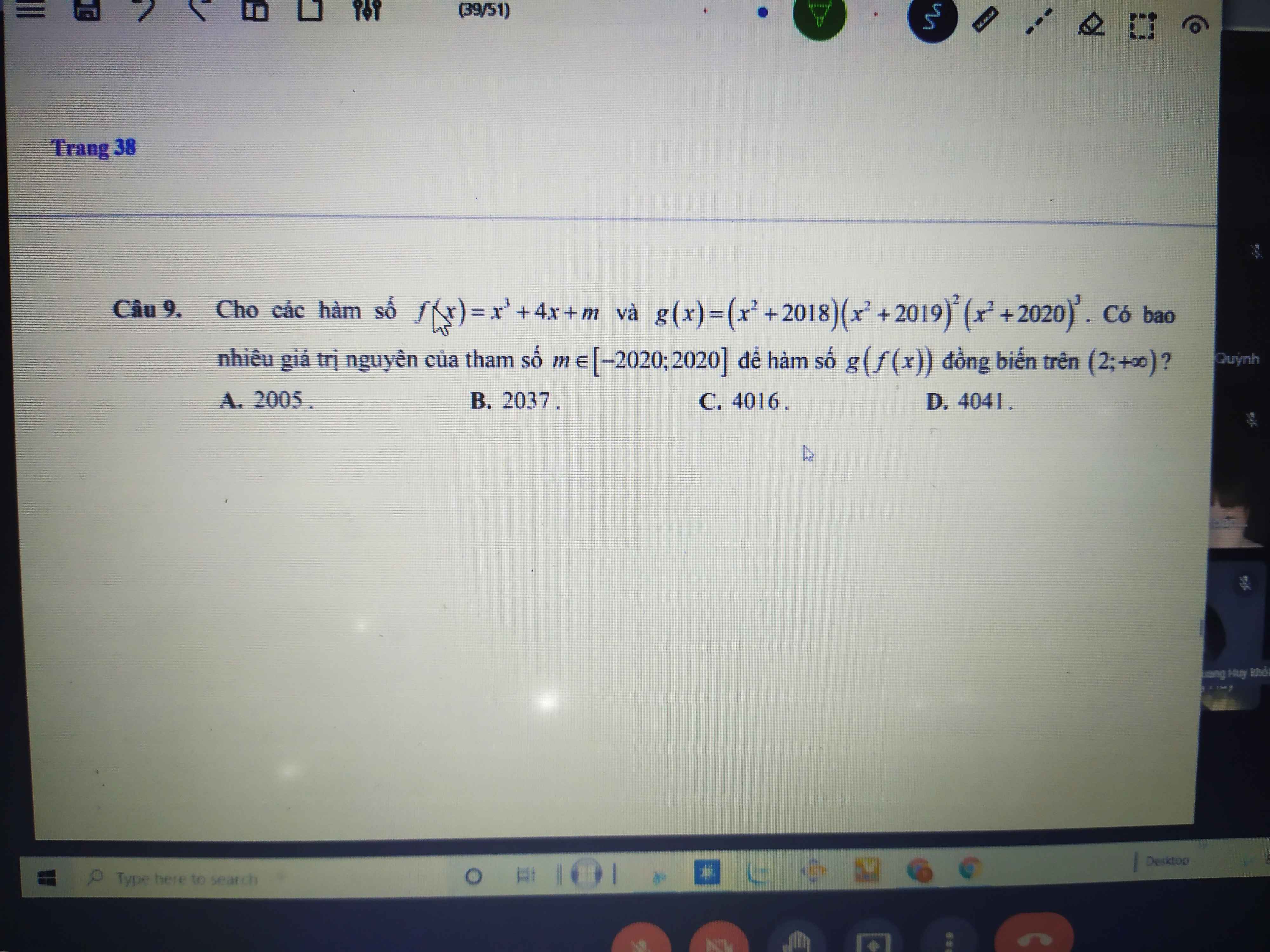
Chú ý quan trọng nhất: biến của \(g\left(x\right)\) là \(x^2\) nên khi đạo hàm \(g'\left(x\right)\) ta sẽ được:
\(g'\left(x\right)=x.h\left(x\right)\) trong đó \(h\left(x\right)\) là 1 hàm luôn dương trên R (là dạng tổng/tích của \(x^2+a\) luôn dương)
Do đó dấu của \(g'\left(x\right)\) chỉ phụ thuộc dấu của x (1)
\(f'\left(x\right)=3x^2+4\) luôn dương
\(y=g\left(f\left(x\right)\right)\Rightarrow y'=f'\left(x\right).g'\left(f\left(x\right)\right)\) chỉ phụ thuộc dấu của \(g'\left(f\left(x\right)\right)\)
Theo (1) thì dấu \(g'\left(f\left(x\right)\right)\) chỉ phụ thuộc dấu \(f\left(x\right)\)
Nên bài toán thỏa mãn khi \(f\left(x\right)\ge0\) ; \(\forall x>2\)
Do \(f\left(x\right)\) đồng biến trên R \(\Rightarrow\min\limits_{x\ge2}f\left(x\right)=f\left(2\right)=m+16\)
\(\Rightarrow m+16\ge0\Rightarrow m\ge-16\)