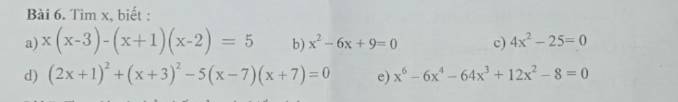Lời giải:
a. $x(x-3)-(x+1)(x-2)=5$
$\Leftrightarrow x^2-3x-(x^2-x-2)=5$
$\Leftrightarrow -2x+2=5$
$\Leftrightarrow -2x=3\Leftrightarrow x=\frac{-3}{2}$
b.
$x^2-6x+9=0$
$\Leftrightarrow (x-3)^2=0\Leftrightarrow x-3=0\Leftrightarrow x=3$
c.
$4x^2-25=0$
$\Leftrightarrow (2x)^2-5^2=0$
$\Leftrightarrow (2x-5)(2x+5)=0$
$\Leftrightarrow 2x-5=0$ hoặc $2x+5=0$
$\Leftrightarrow x=\frac{\pm 5}{2}$
\(\text{#idT50311}\)
`6.`
`a)`
`x(x - 3) - (x + 1)(x - 2) = 5`
`<=> x^2 - 3x - (x^2 - x - 2) = 5`
`<=> x^2 - 3x - x^2 + x + 2 = 5`
`<=> 2 - 2x = 5`
`<=> 2x = -3`
`<=> x = -3/2`
Vậy, `x = -3/2`
`b)`
`x^2 - 6x + 9 = 0`
`<=> x^2 - 2*x*3 + 3^2 = 0`
`<=> (x - 3)^2 = 0`
`<=> x - 3 = 0`
`<=> x = 3`
Vậy, `x = 3`
`c)`
`4x^2 - 25 = 0`
`<=> (2x)^2 - 5^2 = 0`
`<=> (2x -5)(2x + 5) = 0`
`<=>`\(\left[{}\begin{matrix}2x-5=0\\2x+5=0\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}2x=5\\2x=-5\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{5}{2}\end{matrix}\right.\)
Vậy, `x \in {-5/2; 5/2}.`
______
Sử dụng HĐT:
`1)` `(A - B)^2 = A^2 - 2AB + B^2`
`2)` `A^2 - B^2 = (A - B)(A + B)`
`d)`
`(2x + 1)^2 + (x + 3)^2 - 5(x - 7)(x + 7) = 0`
`<=> 4x^2 + 4x + 1 + x^2 + 6x + 9 - 5(x^2 - 7^2) = 0`
`<=> 5x^2 + 10x + 10 - 5x^2 + 5*49 = 0`
`<=> 10x + 10 + 245 = 0`
`<=> 10x + 255 = 0`
`<=> 10x = -255`
`<=> x = -25,5`
Vậy, `x = -25,5`
d.
$(2x+1)^2+(x+3)^2-5(x-7)(x+7)=0$
$\Leftrightarrow (4x^2+4x+1)+(x^2+6x+9)-5(x^2-49)=0$
$\Leftrightarrow 4x^2+4x+1+x^2+6x+9-5x^2+245=0$
$\Leftrightarrow 10x+255=0$
$\Leftrightarrow x=-25,5$
e.
$x^6-6x^4-64x^3+12x^2-8=0$
$\Leftrightarrow (x^2-4x-2)(x^4+4x^3+12x^2-8x+4)=0$
$\Rightarrow x^2-4x-2=0$ hoặc $x^4+4x^3+12x^2-8x+4=0$
Nếu $x^2-4x-2=0$
$\Leftrightarrow (x-2)^2-6=0$
$\Leftrightarrow x-2=\pm \sqrt{6}\Leftrightarrow x=2\pm \sqrt{6}$
-----------------------------
Nếu $x^4+4x^3+12x^2-8x+4=0$
$\Leftrightarrow (x^2+2x)^2+4x^2+4(x-1)^2=0$
$\Rightarrow x^2+2x=x=x-1=0$ (vô lý)
Vậy.........