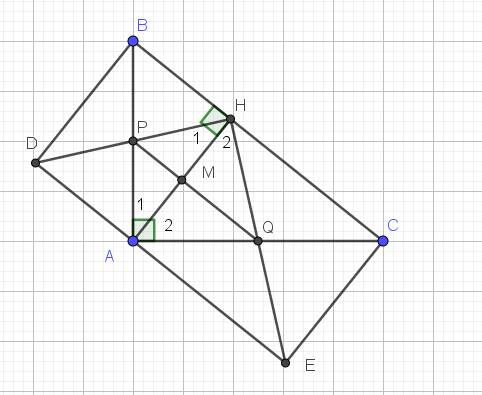
Lời giải:
a.
Vì $AHBD$ là hình chữ nhật nên $\widehat{DAH}=90^0$
Vì $AHCE$ là hình chữ nhật nên $\widehat{HAE}=90^0$
$\Rightarrow \widehat{DAE}=\widehat{DAH}+\widehat{HAE}=90^0+90^0=180^0$
$\Rightarrow D, A, E$ thẳng hàng.
b.
Vì $P,Q$ là trung điểm của $AB, AC$ nên $PQ\parallel BC$
$\Rightarrow PQ\perp AH (1)$
Gọi $M$ là giao điểm $PQ, AH$.
Vì $PQ\parallel BC$ nên $PM\parallel BH$
$\Rightarrow \frac{AM}{MH}=\frac{AP}{PB}=1$
$\Rightarrow AM=MH\Rightarrow M$ là trung điểm $AH(2)$
Từ $(1); (2)\Rightarrow PQ$ là trung trực của $AH$
c.
Vì $AHBD$ là hình chữ nhật nên $DH, AB$ cắt nhau tại trung điểm của mỗi đường. Mà $P$ là trung điểm của $AB$ $\Rightarrow P$ cũng là trung điểm của $DH$
$\Rightarrow P,D,H$ thẳng hàng.
d.
Tương tự phần c ta có $H,Q,E$ thẳng hàng và $Q$ là trung điểm $HE$.
Vì $AHBD$ là hình chữ nhật nên $DH=AB$ và $DH$ cắt $AB$ tại trung điểm $P$ của mỗi đường
$\Rightarrow AP=\frac{1}{2}AB=\frac{1}{2}DH=PH$
$\Rightarrow APH$ là tam giác cân tại $P$
$\Rightarrow \widehat{H_1}=\widehat{A_1}(3)$
Tương tự: $\widehat{H_2}=\widehat{A_2}(4)$
Từ $(3); (4)\Rightarrow \widehat{H_1}+\widehat{H_2}=\widehat{A_1}+\widehat{A_2}$
$\Rightarrow \widehat{DHE}=\widehat{BAC}=90^0$
$\Rightarrow DH\perp EH$