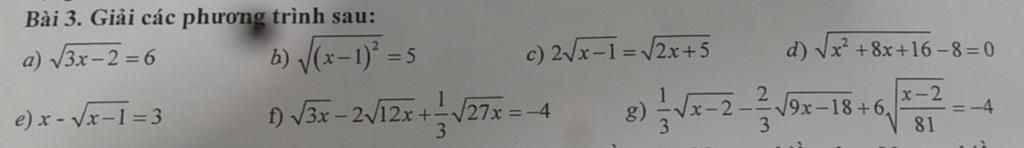`c, 2 sqrt(x-1)=sqrt(2x+5)`
Điều kiện: `x >=1.`
`<=> 4x-4=2x+5`
`<=> 2x=9`
`<=> x=9/2`.
Vậy `x=9/2`.
`d, sqrt(x^2+8x+16)=8`
`<=> |x+4|=8`
`<=> x=4` hoặc `x=-12`.
Vậy ...
`a, sqrt(3x-2)=6`.
Điều kiện: `x >=2/3`.
`<=> 3x-2=36`.
`<=> 3x=38`
`<=> x=38/3`.
Vậy `x=38/3`.
`b, sqrt((x-1)^2)=5`.
`<=> |x-1|=5`
`<=> x-1=5` hoặc `x-1=-5`.
`<=> x=6` hoặc `x=-4`.
Vậy ...
a)
ĐK: \(x\ge\dfrac{2}{3}\)
PT trở thành:
\(3x-2=6^2=36\\ \Leftrightarrow3x=38\\ \Leftrightarrow x=\dfrac{38}{3}\left(tm\right)\)
b)
\(\Leftrightarrow\left|x-1\right|=5\\ \Leftrightarrow\left[{}\begin{matrix}x-1=5\left(với.x\ge5\right)\\1-x=5\left(với.x< 5\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=6\left(tm\right)\\x=1-5=-4\left(tm\right)\end{matrix}\right.\)
c)
ĐK: \(x\ge1\)
PT trở thành:
\(4\left(x-1\right)=2x+5\\ \Leftrightarrow4x-4-2x-5=0\\ \Leftrightarrow2x-9=0\\ \Leftrightarrow x=\dfrac{9}{2}\left(tm\right)\)
d)
\(\Leftrightarrow\sqrt{\left(x+4\right)^2}-8=0\\ \Leftrightarrow\left|x+4\right|=8\\ \Leftrightarrow\left[{}\begin{matrix}x+4=8\left(với.x\ge-4\right)\\x+4=-8\left(với.x< -4\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=4\left(tm\right)\\x=-8-4=-12\left(tm\right)\end{matrix}\right.\)
b) \(\sqrt[]{\left(x-1\right)^2}=5\)
\(\Leftrightarrow\left|x-1\right|=5\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=5\\x-1=-5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-4\end{matrix}\right.\)
d) \(\sqrt[]{x^2+8x+16}-8=0\)
\(\Leftrightarrow\sqrt[]{\left(x+4\right)^2}=8\)
\(\Leftrightarrow\left|x+4\right|=8\)
\(\Leftrightarrow\left[{}\begin{matrix}x+4=8\\x+4=-8\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-12\end{matrix}\right.\)
e) \(x-\sqrt[]{x-1}=3\)
\(\Leftrightarrow\sqrt[]{x-1}=x-3\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-3\ge0\\x-1=\left(x-3\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge3\\x-1=x^2-6x+9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge3\\x^2-7x+10=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge3\\x=2\cup x=5\end{matrix}\right.\)
\(\Leftrightarrow x=5\)