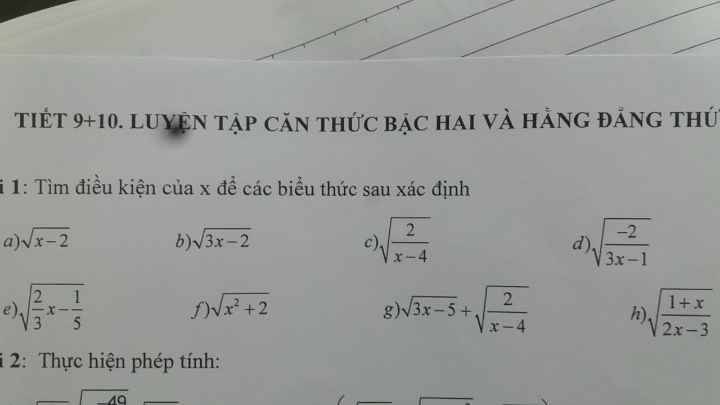`a,` \(\sqrt{x-2}\) xác định khi \(x-2\ge0\Leftrightarrow x\ge2\)
`b,` \(\sqrt{3x-2}\) xác định khi \(3x-2\ge0\Leftrightarrow3x\ge2\Leftrightarrow x\ge\dfrac{2}{3}\)
`c,` \(\sqrt{\dfrac{2}{x-4}}\) xác định khi \(x-4\ge0\Leftrightarrow x\ge4\) vì \(\left(2>0\right)\)
`d,` \(\sqrt{-\dfrac{2}{3x-1}}\) xác định khi \(\left\{{}\begin{matrix}-\dfrac{2}{3x-1}\ge0\\3x-1\ne0\end{matrix}\right.\Leftrightarrow3x-1< 0\Leftrightarrow3x< 1\Leftrightarrow x< \dfrac{1}{3}\)
`e,` \(\sqrt{\dfrac{2}{3}x-\dfrac{1}{5}}\) xác định khi \(\dfrac{2}{3}x-\dfrac{1}{5}\ge0\Leftrightarrow\dfrac{2}{3}x\ge\dfrac{1}{5}\Leftrightarrow x\ge\dfrac{3}{10}\)
\(f,\sqrt{x^2+2}\) Vì `x^2>= 0=> x^2+2 >= 0`
Nên \(\sqrt{x^2+2}\) xác định \(\forall x\)
a) \(\sqrt[]{x-2}\) xác định \(\Leftrightarrow x-2\ge0\Leftrightarrow x\ge2\)
b) \(\sqrt[]{3x-2}\) xác định \(3x-2\ge0\Leftrightarrow x\ge\dfrac{2}{3}\)
c) \(\sqrt[]{\dfrac{2}{x-4}}\) xác định \(\Leftrightarrow\dfrac{2}{x-4}\ge0\Leftrightarrow x-4>0\Leftrightarrow x>4\)
d) \(\sqrt[]{\dfrac{-2}{3x-1}}\) xác định \(\Leftrightarrow\dfrac{-2}{3x-1}\ge0\Leftrightarrow3x-1< 0\Leftrightarrow x< \dfrac{1}{3}\)
e) \(\sqrt[]{\dfrac{2}{3}x-\dfrac{1}{5}}\) xác định \(\Leftrightarrow\dfrac{2}{3}x-\dfrac{1}{5}\ge0\Leftrightarrow\dfrac{2}{3}x\ge\dfrac{1}{5}\Leftrightarrow x\ge\dfrac{3}{10}\)
f) \(\sqrt[]{x^2+2}\) xác định \(\Leftrightarrow x^2+2\ge0\Leftrightarrow\forall x\in R\)
g) \(\sqrt[]{3x-5}+\sqrt[]{\dfrac{2}{x-4}}\) xác định
\(\Leftrightarrow\left\{{}\begin{matrix}3x-5\ge0\\x-4>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{5}{3}\\x>4\end{matrix}\right.\) \(\Leftrightarrow x>4\)
h) \(\sqrt[]{\dfrac{1+x}{2x-3}}\) xác định \(\Leftrightarrow\dfrac{1+x}{2x-3}\ge0\)
\(\Leftrightarrow x\le-1\cup x>\dfrac{3}{2}\)