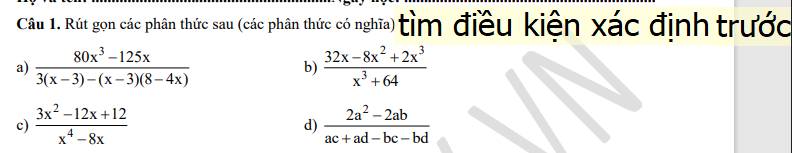a) \(A=\dfrac{80x^3-125x}{3\left(x-3\right)-\left(x-3\right)\left(8-4x\right)}\)
\(A=\dfrac{80x^3-125x}{\left(x-3\right)\left(-5+4x\right)}\) có nghĩa \(\Leftrightarrow\left(x-3\right)\left(-5+4x\right)\ne0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-3\ne0\\-5+4x\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ne3\\x\ne\dfrac{5}{4}\end{matrix}\right.\)
\(\Leftrightarrow A=\dfrac{5x\left(16x^2-25\right)}{\left(x-3\right)\left(-5+4x\right)}\)
\(\Leftrightarrow A=\dfrac{5x\left(4x-5\right)\left(4x+5\right)}{\left(x-3\right)\left(4x-5\right)}\)
\(\Leftrightarrow A=\dfrac{5x\left(4x+5\right)}{x-3}\)
b) \(B=\dfrac{32x-8x^2+2x^3}{x^3+64}\) có nghĩa khi và chỉ khi
\(x^3+64\ne0\Leftrightarrow x^3\ne-64\Leftrightarrow x\ne-4\)
\(\Leftrightarrow B=\dfrac{2x\left(x^2-4x+16\right)}{\left(x+4\right)\left(x^2-4x+16\right)}\)
\(\Leftrightarrow B=\dfrac{2x}{x+4}\)