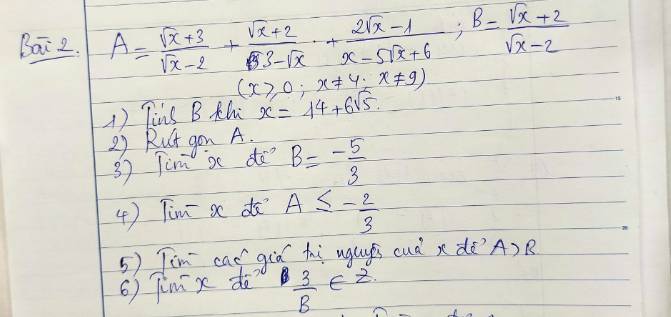2) ĐK: \(x\ge0;x\ne4\)
\(A=\dfrac{\sqrt{x}+3}{\sqrt{x}-2}-\dfrac{\sqrt{x}+2}{\sqrt{x}-3}+\dfrac{2\sqrt{x}-1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)+2\sqrt{x}-1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{x-9-\left(x-4\right)+2\sqrt{x}-1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{2\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{2}{\sqrt{x}-2}\)
Vậy...
1) \(\sqrt{14+6\sqrt{5}}=\sqrt{5+2.3.\sqrt{5}+9}=\sqrt{\left(\sqrt{5}+3\right)^2}=\sqrt{5}+3\)
Thay \(x=14+6\sqrt{5}\) vào B :
\(B=\dfrac{\sqrt{x}+2}{\sqrt{x}-2}=\dfrac{\sqrt{14+6\sqrt{5}}+2}{\sqrt{14+6\sqrt{5}}-2}=\dfrac{3+\sqrt{5}+2}{3+\sqrt{5}-2}\)\(=\dfrac{5+\sqrt{5}}{1+\sqrt{5}}\)
\(=\dfrac{\left(5+\sqrt{5}\right)\left(\sqrt{5}-1\right)}{\left(\sqrt{5}-1\right)\left(\sqrt{5}+1\right)}\)\(=\dfrac{5\sqrt{5}-5+5-\sqrt{5}}{4}=\sqrt{5}\)
Vậy...
3) \(B=-\dfrac{5}{3}\Leftrightarrow\dfrac{\sqrt{x}+2}{\sqrt{x}-2}=-\dfrac{5}{3}\left(ĐK:x\ge0;x\ne4\right)\)
\(\Rightarrow3\sqrt{x}+6=-5\sqrt{x}+10\) \(\Leftrightarrow\sqrt{x}=\dfrac{1}{2}\) \(\Leftrightarrow x=\dfrac{1}{4}\) (tm)
Vậy...
4) \(A\le-\dfrac{2}{3}\Leftrightarrow\dfrac{2}{\sqrt{x}-2}\le-\dfrac{2}{3}\) \(\Leftrightarrow\dfrac{2}{2-\sqrt{x}}\ge\dfrac{2}{3}\Leftrightarrow2-\sqrt{x}\le3\)
\(\Leftrightarrow\sqrt{x}\ge-1\left(lđ\right)\)
Vậy \(\forall x\) thì \(A\le-\dfrac{2}{3}\)
5) \(A>B\Leftrightarrow\dfrac{2}{\sqrt{x}-2}>\dfrac{\sqrt{x}+2}{\sqrt{x}-2}\)
TH1: \(\sqrt{x}-2>0\Leftrightarrow x>4\)
BPT \(\Leftrightarrow2>\sqrt{x}+2\Leftrightarrow0>\sqrt{x}\left(vn\right)\)
TH2: \(\sqrt{x}-2< 0\Leftrightarrow x< 4\)
BPT \(\Leftrightarrow2< \sqrt{x}+2\Leftrightarrow\sqrt{x}>0\Leftrightarrow x>0\)
Vậy \(A< B\Leftrightarrow0< x< 4\Rightarrow x=\left\{1;2;3\right\}\)
6) Đk của B là \(x\ge0;x\ne4\)
\(\dfrac{3}{B}=\dfrac{3\left(\sqrt{x}-2\right)}{\sqrt{x}+2}=\dfrac{3\left(\sqrt{x}+2\right)-12}{\sqrt{x}+2}=3-\dfrac{12}{\sqrt{x}+2}\)
\(\dfrac{3}{B}\in Z\Leftrightarrow\dfrac{12}{\sqrt{x}+2}\in Z\). Ta có \(\sqrt{x}+2\ge2\Leftrightarrow0< \dfrac{12}{\sqrt{x}+2}\le6\)
TH1: \(\dfrac{12}{\sqrt{x}+2}=1\) \(\Leftrightarrow x=100\left(tmđk\right)\)
Tương tự ta được các x thỏa mãn là 16; 1; 0,16; 0
Vậy \(x\in\left\{0,\dfrac{4}{25},1,16,100\right\}\)
[бяїgнтёя тнап а бгцё $кч]