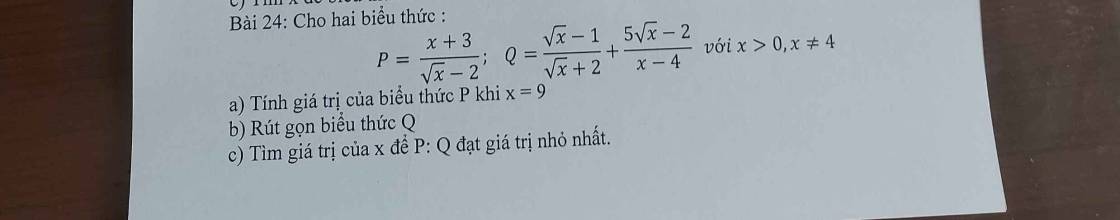\(a,\) Thay \(x=9\) vào P \(\Rightarrow P=\dfrac{9+3}{\sqrt{9}-2}=\dfrac{12}{3-2}=12\)
\(b,Q=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}+\dfrac{5\sqrt{x}-2}{x-4}\left(dkxd:x>0,x\ne4\right)\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}+\dfrac{5\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)+5\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{x-2\sqrt{x}-\sqrt{x}+2+5\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{x+2\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
\(c,P:Q=\dfrac{x+3}{\sqrt{x}-2}:\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
\(=\dfrac{x+3}{\sqrt{x}-2}.\dfrac{\sqrt{x}-2}{\sqrt{x}}\)
\(=\dfrac{x+3}{\sqrt{x}}\)
Áp dụng BDT Cô si, ta có \(P:Q=\dfrac{x+3}{\sqrt{x}}=\sqrt{x}+\dfrac{3}{\sqrt{x}}\ge2\sqrt{\sqrt{x}.\dfrac{3}{\sqrt{x}}}\) \(\left(x>0\right)\)
\(\Leftrightarrow P:Q\ge2\sqrt{3}\)
Vậy gia trị nhỏ nhất của \(P:Q=2\sqrt{3}\)
Sửa câu (c):
Có: \(\dfrac{P}{Q}=\dfrac{x+3}{\sqrt{x}-2}:\dfrac{\sqrt{x}}{\sqrt{x}-2}=\dfrac{\left(x+3\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\sqrt{x}}=\dfrac{x+3}{\sqrt{x}}\) \(\ge\dfrac{2\sqrt{x.3}}{\sqrt{x}}=2\sqrt{3}\) (Áp dụng BĐT AM - GM)
Dấu "=" xảy ra \(\Leftrightarrow x=3\)
Vậy x = 3 là giá trị cần tìm, khi đó GTNN của \(\dfrac{P}{Q}=2\sqrt{3}\)