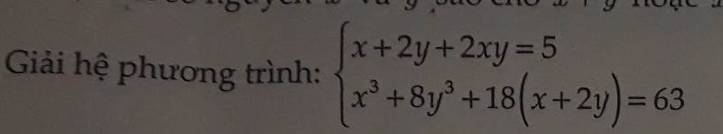\(\left\{{}\begin{matrix}x+2y+2xy=5\left(1\right)\\x^3+8y^3+18\left(x+2y\right)=63\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2xy=5-\left(x+2y\right)\\\left(x+2y\right)^3-3.2xy\left(x+2y\right)+18\left(x+2y\right)=63\end{matrix}\right.\)
\(\Rightarrow\left(x+2y\right)^3-3\left[5-\left(x+2y\right)\right]\left(x+2y\right)+18\left(x+2y\right)=63\)
Đặt \(a=x+2y\). Phương trình trở thành:
\(a^3-3\left(5-a\right)a+18a-63=0\)
\(\Leftrightarrow a^3+3a^2+3a-63=0\)
\(\Leftrightarrow\left(a+1\right)^3=64\)
\(\Leftrightarrow a+1=4\Leftrightarrow a=3\)
\(\Rightarrow x+2y=3\). Thay vào (1) ta được:
\(3+2xy=5\Rightarrow2xy=2\). Ta có: \(\left\{{}\begin{matrix}x+2y=3\\x.2y=2\end{matrix}\right.\)
\(\Rightarrow x,2y\) là 2 nghiệm của phương trình \(X^2-3X+2=0\left(2\right)\)
Mặt khác giải phương trình (1) ta được: \(X_1=1;X_2=2\)
\(\Rightarrow\left(x;2y\right)=\left(1;2\right),\left(2;1\right)\)
\(\Rightarrow\left(x;y\right)=\left(1;1\right),\left(2;\dfrac{1}{2}\right)\)
Vậy hệ phương trình đã cho có các nghiệm (x;y) là \(\left(1;1\right),\left(2;\dfrac{1}{2}\right)\)