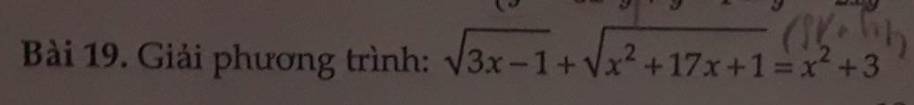Lời giải:
ĐKXĐ: $x\geq \frac{1}{3}$
PT $\Leftrightarrow x^2+3-\sqrt{3x-1}-\sqrt{x^2+17x+1}=0$
$\Leftrightarrow (x^2-3x+1)+(x-\sqrt{3x-1})+[(2x+2)-\sqrt{x^2+17x+1}]=0$
$\Leftrightarrow (x^2-3x+1)+\frac{x^2-3x+1}{x+\sqrt{3x-1}}+\frac{3(x^2-3x+1)}{2x+2+\sqrt{x^2+17x+1}}=0$
$\Leftrightarrow (x^2-3x+1)\left[1+\frac{1}{x+\sqrt{3x-1}}+\frac{3}{2x+2+\sqrt{x^2+17x+1}}\right]=0$
Dễ thấy với $x\geq \frac{1}{3}$ thì biểu thức trong ngoặc vuông luôn lớn hơn $0$
$\Rightarrow x^2-3x+1=0$
$\Leftrightarrow x=\frac{1}{2}(3\pm \sqrt{5})$
Đúng 1
Bình luận (0)
