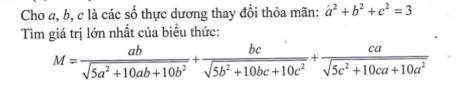Có: \(5a^2+10ab+10b^2=\left(2a+3b\right)^2+\left(a-b\right)^2\ge\left(2a+3b\right)^2\), dấu "=" xảy ra khi a = b
=> \(\sqrt{5a^2+10ab+10b^2}\ge2a+3b\)
hay \(\dfrac{ab}{\sqrt{5a^2+10ab+10b^2}}\le\dfrac{ab}{2a+3b}\)
Chứng minh: \(\dfrac{ab}{2a+3b}\le\dfrac{3a+2b}{25}\)
Thật vậy: \(25ab\le\left(2a+3b\right)\left(3a+2b\right)\Leftrightarrow6\left(a-b\right)^2\ge0\) (luôn đúng), dấu "=" xảy ra khi a = b.
Do đó: \(\dfrac{ab}{\sqrt{5a^2+10ab+10b^2}}\le\dfrac{3a+2b}{25}\)
Tương tự ta có:
\(\)\(\dfrac{bc}{\sqrt{5b^2+10bc+10c^2}}\le\dfrac{3b+2c}{25}\)
\(\dfrac{ca}{\sqrt{5c^2+10ca+10a^2}}\le\dfrac{3c+2a}{25}\)
Cộng các bđt trên, được:
\(M\le\dfrac{3a+2b}{25}+\dfrac{3b+2c}{25}+\dfrac{3c+2a}{25}=\dfrac{1}{5}\left(a+b+c\right)\)
Có: \(\left(a+b+c\right)^2=a^2+b^2+c^2+2ab+2bc+2ca\le a^2+b^2+c^2+\left(a^2+b^2\right)+\left(b^2+c^2\right)+\left(c^2+a^2\right)\)
\(=3a^2+3b^2+3c^2=9\)
=> \(a+b+c\le3\)
=> \(M\le\dfrac{3}{5}\)
max M \(=\dfrac{3}{5}\) khi a = b = c = 1.
\(\dfrac{ab}{\sqrt{5a^2+10ab+10b^2}}=\dfrac{ab}{\sqrt{5\left[b^2+\left(a+b\right)^2\right]}}=\dfrac{ab}{\sqrt{\left[b^2+\left(a+b\right)^2\right]\left(1^2+2^2\right)}}\le^{Bunhiacopxki}\dfrac{ab}{b.1+\left(a+b\right).2}=\dfrac{ab}{2a+3b}\)
\(\Rightarrow\dfrac{ab}{\sqrt{5a^2+10ab+10b^2}}\le\dfrac{ab}{2a+3b}\left(1\right)\)
Áp dụng bất đẳng thức Bunhiaxcopki dạng phân thức:
\(\dfrac{1}{a}+\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{b}+\dfrac{1}{b}\ge\dfrac{5^2}{2a+3b}\)
\(\Rightarrow\dfrac{25}{2a+3b}\le\dfrac{2}{a}+\dfrac{3}{b}\Rightarrow\dfrac{ab}{2a+3b}\le\dfrac{2b+3a}{25}\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow\dfrac{ab}{\sqrt{5a^2+10ab+10b^2}}\le\dfrac{2b+3a}{25}\left(3\right)\)
Tương tự:
\(\dfrac{bc}{\sqrt{5b^2+10bc+10c^2}}\le\dfrac{2c+3b}{25}\left(4\right)\)
\(\dfrac{ca}{\sqrt{5c^2+10ca+10a^2}}\le\dfrac{2a+3c}{25}\left(5\right)\)
\(\left(3\right)+\left(4\right)+\left(5\right)\Rightarrow M\le\dfrac{a+b+c}{5}\)
Ta có: \(\left(a+b+c\right)^2\le3\left(a^2+b^2+c^2\right)=3.3=9\)
\(\Rightarrow a+b+c\le3\)
\(\Rightarrow M\le\dfrac{a+b+c}{5}\le\dfrac{3}{5}\)
Dấu "=" xảy ra khi \(a=b=c=1\)
Vậy \(MaxM=\dfrac{3}{5}\)