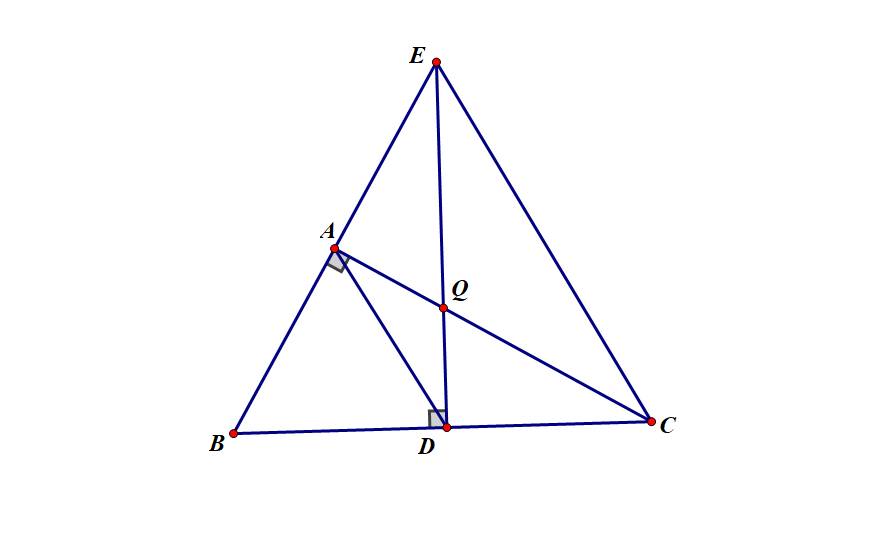
a. Xét \(2\Delta:\Delta ABC\) và \(\Delta DQC\) có:
\(\left\{{}\begin{matrix}\widehat{BAC}=\widehat{QDC}=90^o\\\widehat{ACB}.chung\end{matrix}\right.\)
\(\Rightarrow\Delta ABC\sim\Delta DQC\left(g-g\right)\)
\(\Rightarrow\dfrac{CA}{CB}=\dfrac{CD}{CQ}\Leftrightarrow CD.CB=CQ.CA\)
b. Xét \(2\Delta:\Delta DQC\) và \(\Delta AQE\) có:
\(\left\{{}\begin{matrix}\widehat{EAQ}=\widehat{CDQ}=90^o\\\widehat{AQE}=\widehat{DQC}\left(đối.đỉnh\right)\end{matrix}\right.\)
\(\Rightarrow\Delta DQC\sim\Delta AQE\left(g-g\right)\)
\(\Rightarrow\dfrac{QC}{QD}=\dfrac{QE}{QA}\Leftrightarrow QA.QC=QD.QE\)
Ta lại có: \(\Delta ABC\sim\Delta DQC\)
\(\Rightarrow\Delta ABC\sim\Delta AQE\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{AQ}{AE}\Leftrightarrow AB.AE=AQ.AC\)
c. Dựa vào câu a và b, ta có:
\(AB.AE+CB.CD=AQ.AC+CQ.CA=AC\left(AQ+CQ\right)=AC.AC=AC^2\)
d. Xét \(2\Delta:\Delta QEC\) và \(\Delta QAD\) có:
\(\left\{{}\begin{matrix}\widehat{AQD}=\widehat{CQE}\left(đối.đỉnh\right)\\\dfrac{QC}{QD}=\dfrac{QE}{QA}\left(câu.b\right)\end{matrix}\right.\)
\(\Rightarrow\Delta QEC\sim\Delta QAD\left(c-g-c\right)\)
\(\Rightarrow\widehat{QAD}=\widehat{QEC}\)
Dễ chứng minh: \(\Delta AQE=\Delta DQC\Rightarrow\Delta QEC.cân\)
\(\Rightarrow\Delta QAD.cân\)
\(\Rightarrow AD//EC\left(slt\right)\)
\(\Rightarrow\widehat{BAD}=\widehat{BEC}\left(đv\right)\left(1\right)\)
Mà ta có: \(\widehat{AEQ}+\widehat{QEC}=\widehat{DCQ}+\widehat{QCE}\) hay \(\widehat{BEC}=\widehat{BCE}\left(2\right)\)
Từ (1) và (2), suy ra: \(\widehat{BAD}=\widehat{BCE}\)