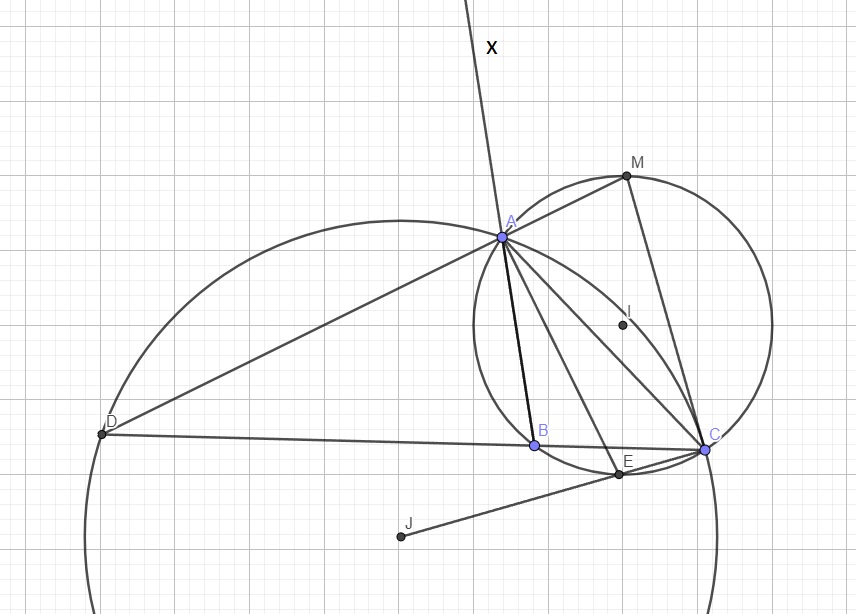
Sửa đề: D là phân giác trong
góc CJD=2*góc CAD
=>góc CJD=2*góc BAD=2*góc BCM
=>góc CJD=2*góc BCM
=>ΔCJD cân tại J
=>góc CJD+2*góc JCD=180 độ
=>góc BCM+góc JCD=90 độ
=>CM vuông góc CJ
=>CJ: x-y+4=0
Tọa độ C là:
x-y+4=0 và x+y-2=0
=>x=-1 và y=3
A,C là hai điểm chung của (I) và (J) nên AC đi qua C và vuông góc IJ
=>AC: x=-1
(C) ngoại tiếp ΔACB có tâm I(2;2); ban kính IC=căn 10
(C): (x-2)^2+(y-2)^2=10
Tọa độ A là:
(x-2)^2+(y-2)^2=10 và x=-1
=>x=-1 và y=1
Do M=CM cắt (C) nên M(3;-1) là điểm chính giữa của cung BC
=>IM vuông góc BC
BC đi qua C, vuông góc IM
nên BC: x-3y+10=0
B=BC giao (C)
nên B(19/5;23/5)
Thôi chứng minh luôn cho em, rồi hướng dẫn đoạn tính toán em tự tính:
Gọi phân giác trong góc A cắt đường tròn ngoại tiếp ABC tại E
Do AM là phân giác ngoài và AE là phân giác trong
\(\Rightarrow\widehat{MAC}+\widehat{CAE}=\dfrac{1}{2}\widehat{xAC}+\dfrac{1}{2}\widehat{CAB}=\dfrac{1}{2}.180^0=90^0\)
\(\Rightarrow\widehat{MAE}=90^0\Rightarrow ME\) là đường kính hay M, I, E thẳng hàng.
\(\Rightarrow\widehat{DAE}=180^0-\widehat{MAE}=90^0\Rightarrow\widehat{DAE}=\widehat{MAE}\)
Mà \(\left\{{}\begin{matrix}\widehat{BAE}=\widehat{CAE}\\\widehat{BAD}=\widehat{DAE}-\widehat{BAE}\\\widehat{MAC}=\widehat{MAE}-\widehat{CAE}\end{matrix}\right.\) \(\Rightarrow\widehat{BAD}=\widehat{MAC}\) (1)
Lại có \(\widehat{ABD}=\widehat{CMA}\) (cùng bù \(\widehat{ABC}\)) (2)
(1);(2) \(\Rightarrow\widehat{ADB}=\widehat{ACM}\) (2 tam giác có 2 góc bằng nhau thì góc còn lại cũng bằng nhau)
Mà \(\widehat{ADB}\) và \(\widehat{ACM}\) cùng chắn cung AC của đường tròn ngoại tiếp ACD
\(\Rightarrow MC\) là tiếp tuyến hay \(MC\perp JC\) \(\Rightarrow J,E,C\) thẳng hàng (cùng vuông góc MC)
\(\Rightarrow\) Viết được phương trình JC (qua J và vuông góc đường thẳng MC đã biết)
\(\Rightarrow\) Tìm được tọa độ C là giao JC và MC
\(\Rightarrow\) Tính được \(IC;JC\Rightarrow\) viết được pt đường tròn ngoại tiếp ABC và ACD
\(\Rightarrow\) Tìm được tọa độ A (là giao điểm thứ 2 của hai đường tròn nói trên)
\(\Rightarrow\) Tìm được tọa độ E (giao của JC và đường tròn (ABC))
\(\Rightarrow\) Viết được pt BC (qua C và vuông góc IE)
\(\Rightarrow\) Tìm được tọa độ B