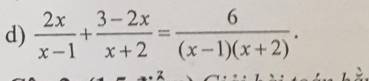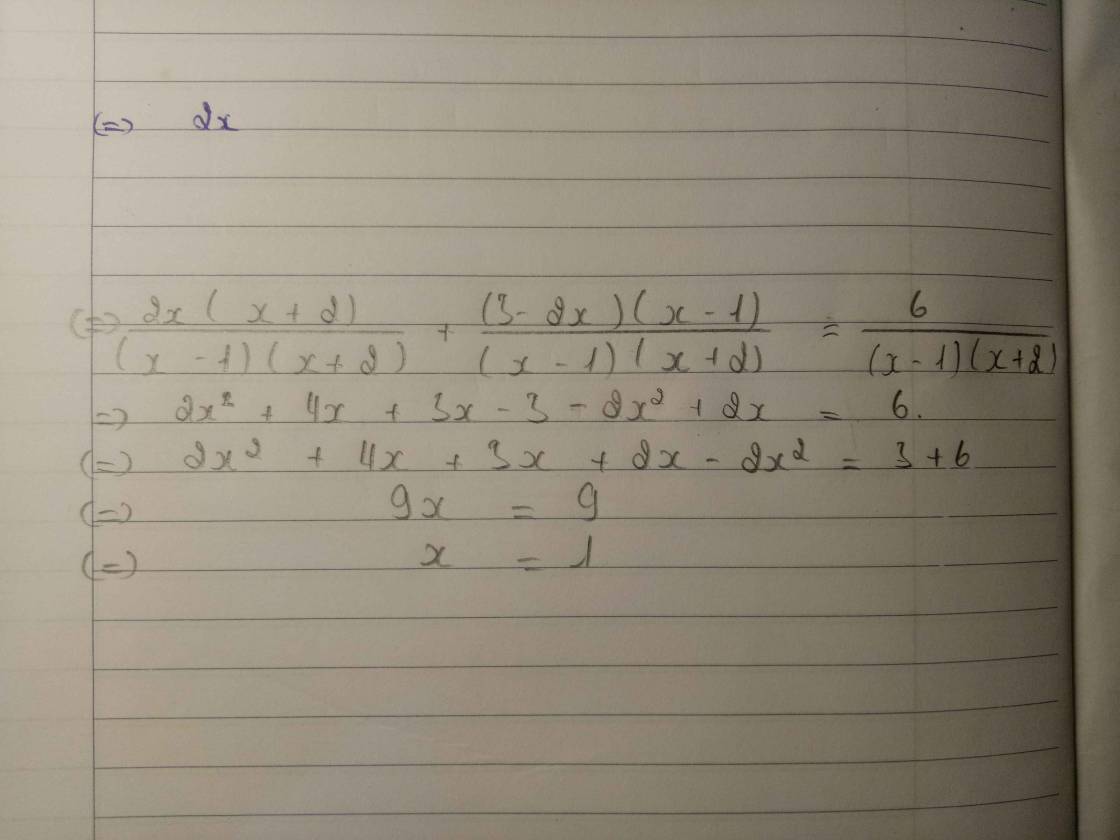\(\dfrac{2x}{x-1}+\dfrac{3-2x}{x+2}=\dfrac{6}{\left(x-1\right)\left(x+2\right)}\)
ĐKXĐ : \(\left\{{}\begin{matrix}x-1\ne0\\x+2\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne1\\x\ne-2\end{matrix}\right.\)
Ta có : \(\dfrac{2x}{x-1}+\dfrac{3-2x}{x+2}=\dfrac{6}{\left(x-1\right)\left(x+2\right)}\)
\(\Leftrightarrow\dfrac{2x\left(x+2\right)}{\left(x-1\right)\left(x+2\right)}+\dfrac{\left(3-2x\right)\left(x-1\right)}{\left(x-1\right)\left(x+2\right)}=\dfrac{6}{\left(x-1\right)\left(x+2\right)}\)
`=> 2x^2 + 4x + 3x-3-2x^2+2x -6=0`
`<=> 9x-9=0`
`<=>9x=9`
`<=>x=1 (t/m)`
\(\dfrac{2x}{x-1}+\dfrac{3-2x}{x+2}=\dfrac{6}{\left(x-1\right)\left(x+2\right)}\left(dkxd:x\ne1;x\ne-2\right)\)
\(\Leftrightarrow\dfrac{2x}{x-1}+\dfrac{3-2x}{x+2}-\dfrac{6}{\left(x-1\right)\left(x+2\right)}=0\)
\(\Leftrightarrow2x\left(x+2\right)+\left(3-2x\right)\left(x-1\right)-6=0\)
\(\Leftrightarrow2x^2+4x+3x-3-2x^2+2x-6=0\)
\(\Leftrightarrow9x=9\)
\(\Leftrightarrow x=1\left(ktmdk\right)\)
Vậy pt vô nghiệm
(ĐKXĐ x≠1;x≠-2)
(=)\(\dfrac{\left(x+2\right).2x+\left(3-2x\right)\left(x-1\right)}{\left(x-1\right)\left(x+2\right)}=\dfrac{6}{\left(x-1\right)\left(x+2\right)}\)
⇒2x2+ 4x+ 5x- 3- 2x2= 6
(=) 2x2+ 4x+ 5x- 2x2= 6+ 3
(=) 9x= 9
(=) x=1 (ko t/m)
Vậy PT có nghiệm là ∅
=>2x(x+2)+(3-2x)(x-1)=6
<=>2x2+4+3x-3-2x2+2x=6
<=>2x2+3x-2x2+2x=6-4+3
<=>5x=5
<=>x=5