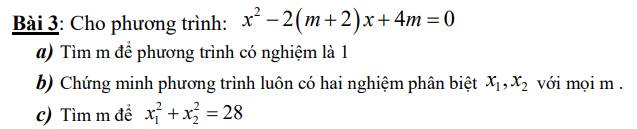a)
Để pt có nghiệm `x=1`
`<=> 1^2 -2(m+2)*1+4m=0`
`<=> 1 - 2(m+2)+4m=0`
`<=> 1-2m-4+4m=0`
`<=> 2m-3=0`
`<=>m=3/2`
Vậy `m=3/2` thì pt có nghiệm `x=1`
b)
`\Delta'=(m+2)^2 - 1*4m = m^2 + 4m+4-4m=m^2+4>0AAm`
Vậy pt luôn có hai nghiệm phân biệt với mọi `m`
c)
Theo định lý Vi-ét : `{(x_1 + x_2 = 2( m+2)),(x_1x_2 = 4m):}`
`=> ( x_1)^2 + ( x_2)^2 = ( x_1+x_2)^2 - 2x_1x_2=4(m+2)^2-8m`
Mà `( x_1)^2 + ( x_2)^2=28 => 4(m+2)^2-8m=28`
`<=> m^2+4m+4-2m=7`
`<=> m^2+2m+4=7`
`<=> ( m+1)^2=4=(+-2)^2`
`<=> [(m+1=2),(m+1=-2):}<=>[(m=1),(m=-3):}`
Vậy `m in { 1;-3}` thì `( x_1)^2 + ( x_2)^2=28`