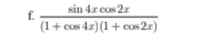a.
\(=\left(1+tan^2x\right)-tan^2x-cos^2x\)
\(=1-cos^2x=sin^2x\)
b.
\(=\dfrac{cos^2x-sin^2x}{\dfrac{cos^2x}{sin^2x}-\dfrac{sin^2x}{cos^2x}}-cos^2x=\dfrac{sin^2x.cos^2x\left(cos^2x-sin^2x\right)}{cos^4x-sin^4x}-cos^2x\)
\(=\dfrac{sin^2x.cos^2x\left(cos^2x-sin^2x\right)}{\left(cos^2x-sin^2x\right)\left(cos^2x+sin^2x\right)}-cos^2x=sin^2x.cos^2x-cos^2x\)
\(=cos^2x\left(sin^2x-1\right)=cos^2x.\left(-cos^2x\right)=-cos^4x\)
c.
\(=\dfrac{\left(sinx+cosx\right)\left(cos^2x+sin^2x-sinx.cosx\right)}{cos^2x+sin^2x-sinx.cosx}=sinx+cosx\)
d.
\(=\dfrac{1+sinx+1-sinx}{\sqrt{\left(1-sinx\right)\left(1+sinx\right)}}=\dfrac{2}{\sqrt{1-cos^2x}}=\dfrac{2}{\sqrt{sin^2x}}=\dfrac{2}{\left|sinx\right|}\)
e.
\(=\sqrt{\dfrac{1-cosx+1+cosx}{\left(1+cosx\right)\left(1-cosx\right)}}.\sqrt{\dfrac{1-sinx+1+sinx}{\left(1+sinx\right)\left(1-sinx\right)}}\)
\(=\sqrt{\dfrac{2}{1-cos^2x}}.\sqrt{\dfrac{2}{1-sin^2x}}=2\sqrt{\dfrac{1}{sin^2x}}.\sqrt{\dfrac{1}{cos^2x}}=\dfrac{2}{\sqrt{sin^2x.cos^2x}}\)
\(=\dfrac{2}{\sqrt{\dfrac{1}{4}sin^22x}}=\dfrac{4}{\left|sin2x\right|}\)
f.
\(=\left(\dfrac{1}{sin^2x}+\dfrac{1}{cos^2x}-\dfrac{sin^2x}{cos^2x}-\dfrac{cos^2x}{sin^2x}\right)\left(\dfrac{1}{sin^2x}-\dfrac{1}{cos^2x}\right)\)
\(=\left[\dfrac{1}{sin^2x}\left(1-cos^2x\right)+\dfrac{1}{cos^2x}\left(1-sin^2x\right)\right]\left(\dfrac{1}{sin^2x}-\dfrac{1}{cos^2x}\right)\)
\(=\left(\dfrac{sin^2x}{sin^2x}+\dfrac{cos^2x}{cos^2x}\right)\left(\dfrac{cos^2x-sin^2x}{sin^2x.cos^2x}\right)=\dfrac{2.cos2x}{\dfrac{1}{4}sin^22x}=\dfrac{8cot2x}{sin2x}\)