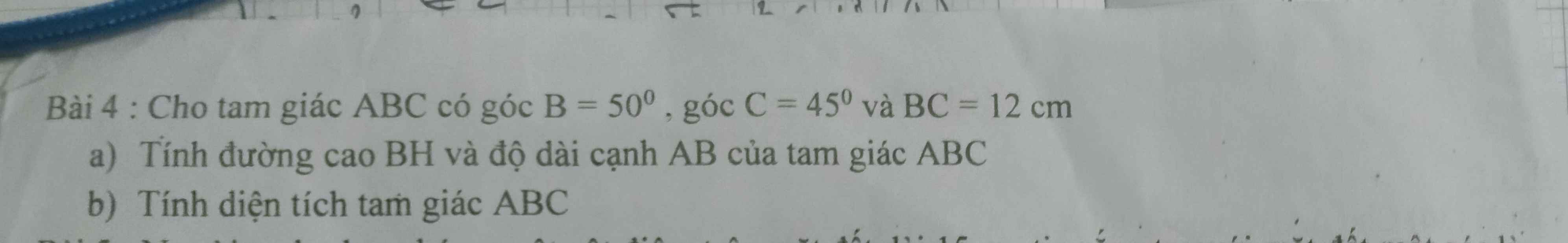a)
Ta có:
BH là đường cao(gt) => BH \(\perp\) AC =>\(\widehat{BHC}=90^0\)
Xét tam giác BHC có:
\(\widehat{C}+\widehat{BHC}+\widehat{CBH}=180^0\) ( tính chất tổng 3 góc trong 1 tam giác )
\(\Rightarrow\widehat{CBH}=180^0-\widehat{C}-\widehat{BHC}\)
\(\Rightarrow\widehat{CHB}=180^0-45^0-90^0\)
\(\Rightarrow\widehat{CHB}=45^0\) (1)
mà : \(\widehat{BCH}=45^0\) (2)
Từ(1) và (2) => \(\widehat{CHB}=\widehat{BCH}=45^0\)(2 góc này là 2 góc đáy của \(\Delta BHC\))
=> tam giác BHC cân tại H => BH=CH (t/c 2 cạnh bên trong tam giác cân)
Ta lại có:
Tam giác BHC có:
góc BHC = 90 độ
=> tam giác BHC vuông tại H => BC là cạnh huyền của tam giác BHC
=>\(BC^2=BH^2+CH^2\) ( t/c cạnh huyền )
Mà BH=CH (cmt)
=> \(BC^2=BH^2+BH^2=2BH^2=2CH^2\)
=> \(12^2=2BH^2=2CH^2\)
=> \(144=2BH^2=2CH^2\)
=> \(BH^2=CH^2=144:2\left(cm\right)\)
=> \(BH^2=CH^2=72\left(cm\right)\)
=> \(BH=CH=\sqrt{72}\left(cm\right)=8\left(cm\right)\)