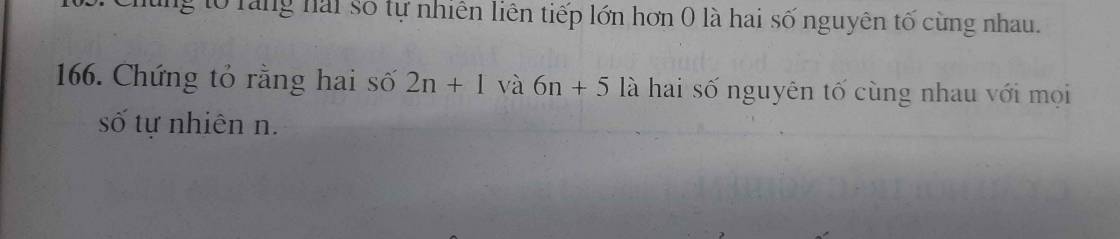Gọi ƯCLN(2n+1, 6n+5)=d
Có: \(\left\{{}\begin{matrix}2n+1⋮d\\6n+5⋮d\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}3\left(2n+1\right)⋮d\\6n+5⋮d\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}6n+3⋮d\\6n+5⋮d\end{matrix}\right.\)
\(\Rightarrow\left(6n+5\right)-\left(6n+3\right)⋮d\)
\(\Rightarrow2⋮d\)
mà \(2n+1⋮̸2;6n+5⋮̸2\)
\(\Rightarrow\) `2n+1` và `6n+5` là nguyên tố cùng nhau (đpcm)
Đúng 1
Bình luận (0)