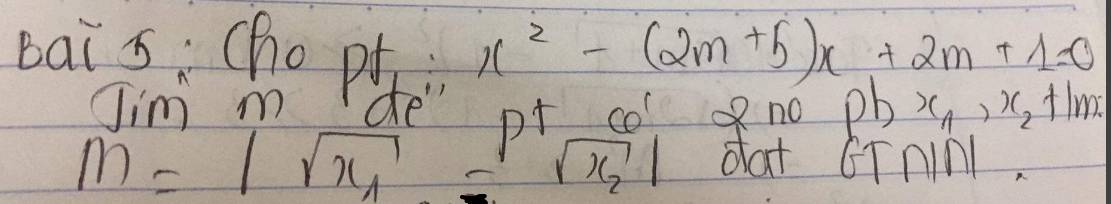Đk pt có 2 nghiệm pb là:
\(\Delta=\left(2m+5\right)^2-4\left(2m+1\right)>0\)
\(\Leftrightarrow\left(2m+5\right)^2-4\left(2m+5\right)+4>0\)
\(\Leftrightarrow\left(2m+7\right)^2>0\)
\(\Leftrightarrow2m+7\ne0\)
\(\Leftrightarrow m\ne-\dfrac{7}{2}\)
Theo hệ thức Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=2m+5\\x_1x_2=2m+1\end{matrix}\right.\)
Vì pt có 2 nghiệm pb x1, x2 thỏa mãn \(M=\left|\sqrt{x_1}-\sqrt{x_2}\right|\) đạt GTNN nên điều kiện xác định là: \(\left\{{}\begin{matrix}x_1\ge0\\x_2\ge0\end{matrix}\right.\Leftrightarrow x_1x_2\ge0\Leftrightarrow2m+1\ge0\Leftrightarrow m\ge-\dfrac{1}{2}\)
Ta có:
\(M=\left|\sqrt{x_1}-\sqrt{x_2}\right|\)
\(=\sqrt{\left(\sqrt{x_1}-\sqrt{x_2}\right)^2}\)
\(=\sqrt{x_1+x_2-2\sqrt{x_1x_2}}\)
\(=\sqrt{2m+5-2\sqrt{2m+1}}\)
\(=\sqrt{2m+1-2\sqrt{2m+1}+1+3}\)
\(=\sqrt{\left(\sqrt{2m+1}-1\right)^2+3}\ge\sqrt{3}\)
Dấu "=" xảy ra \(\Leftrightarrow\sqrt{2m+1}=1\Leftrightarrow2m+1=1\Leftrightarrow m=0\) (nhận)
Vậy MinM = \(\sqrt{3}\) <=> m = 0