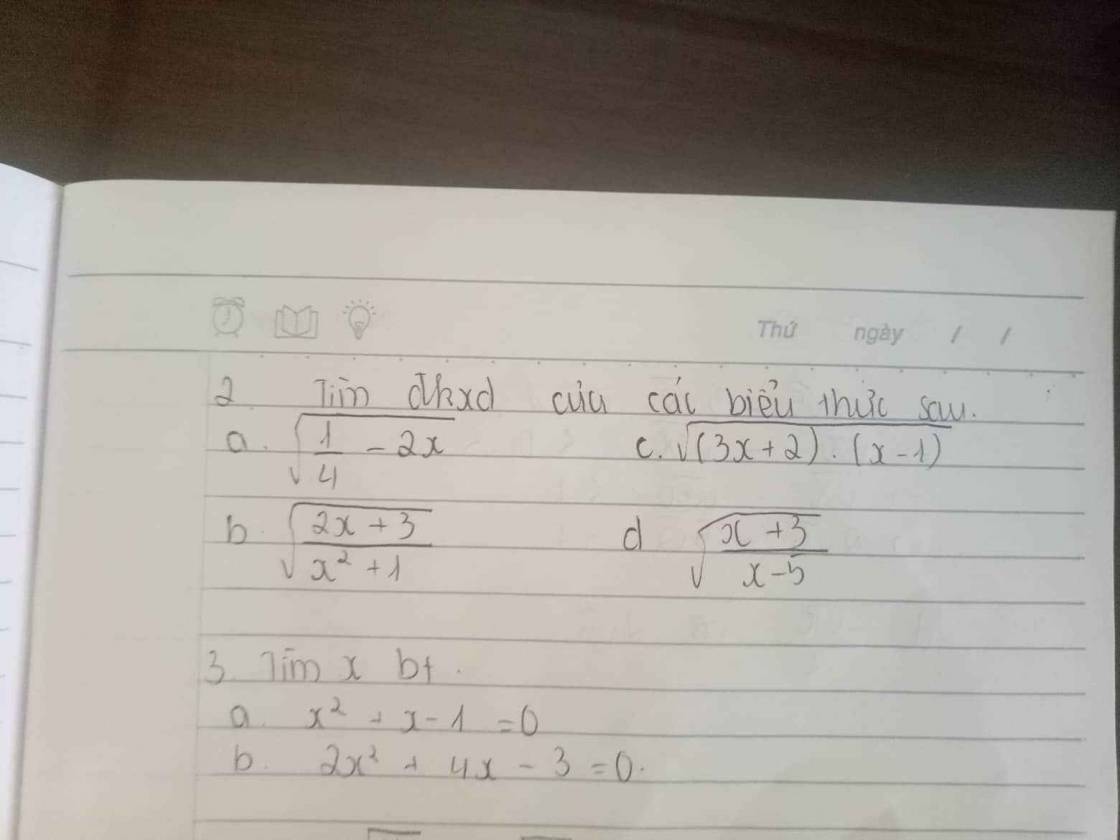3, a, x^2 + x - 1 = 0
\(\Leftrightarrow x^2+x+\dfrac{1}{4}-\dfrac{1}{4}-1=0\Leftrightarrow\left(x+\dfrac{1}{2}\right)^2-\dfrac{5}{4}=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{5}}{2}-\dfrac{1}{2}\\x=-\dfrac{\sqrt{5}}{2}-\dfrac{1}{2}\end{matrix}\right.\)
4, \(2\left(x^2+2x+1-1\right)-3=0\Leftrightarrow2\left(x+1\right)^2-5=0\)
\(\Leftrightarrow\left(\sqrt{2}x+\sqrt{2}\right)^2-5=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{5}-\sqrt{2}}{\sqrt{2}}=\dfrac{\sqrt{10}}{2}-1\\x=-\dfrac{\sqrt{10}}{2}-1\end{matrix}\right.\)
Bài 2:
a. ĐKXĐ: $\frac{1}{4}-2x\geq 0$
$\Leftrightarrow x\leq \frac{1}{8}$
b. ĐKXĐ: $(3x+2)(x-1)\geq 0$
\(\Leftrightarrow \left[\begin{matrix} \left\{\begin{matrix} 3x+2\geq 0\\ x-1\geq 0\end{matrix}\right.\\ \left\{\begin{matrix} 3x+2\leq 0\\ x-1\leq 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x\geq 1\\ x\leq \frac{-2}{3}\end{matrix}\right.\)
c.
ĐKXĐ: \(\left\{\begin{matrix} x^2+1\neq 0\\ \frac{2x+3}{x^2+1}\geq 0\end{matrix}\right.\Leftrightarrow 2x+3\geq 0\) (do $x^2+1>0$ với mọi $x\in\mathbb{R}$)
$\Leftrightarrow x\geq \frac{-3}{2}$
d.
\(\left\{\begin{matrix} x-5\neq 0\\ \frac{x+3}{x-5}\geq 0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} \left\{\begin{matrix} x+3\leq 0\\ x-5<0\end{matrix}\right.\\ \left\{\begin{matrix} x+3\geq 0\\ x-5>0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x\leq -3\\ x>5\end{matrix}\right.\)
Bài 3:
a. $x^2+x-1=0$
$\Leftrightarrow 4x^2+4x-4=0$
$\Leftrightarrow (2x+1)^2-5=0$
$\Leftrightarrow 2x+1=\pm \sqrt{5}$
$\Leftrightarrow x=\frac{-1\pm \sqrt{5}}{2}$
b.
$2x^2+4x-3=0$
$\Leftrightarrow 2(x^2+2x+1)-5=0$
$\Leftrightarrow 2(x+1)^2=5$
$\Leftrightarrow (x+1)^2=\frac{5}{2}$
$\Leftrightarrow x+1=\pm \sqrt{\frac{5}{2}}$
$\Leftrightarrow x=-1\pm \sqrt{\frac{5}{2}}$