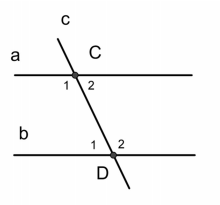
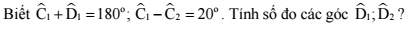Ta có :
\(\widehat{C_1}+\widehat{C_2}=180^o\)
\(\widehat{C_1}-\widehat{C_2}=20^o\)
\(\Rightarrow\widehat{C_1}=\left(180+20\right):2=100^O\)
\(\Rightarrow\widehat{C_2}=180^o-100^o=80^o\)
\(\Rightarrow\widehat{D_1}=180^o-\widehat{C_1}=80^o\)
\(\Rightarrow\widehat{D_2}=180^o-\widehat{D_1}=100^o\)
vì \(\widehat{C_1}+\widehat{D_1}=180^0\)
mà hai góc này ở vị trí trong cùng phía
nên a \(//\) b
lại có \(\widehat{C_1}+\widehat{C_2}=180^0\)(kề bù)
mà \(\widehat{C_1}-\widehat{C_2}=20^0\)
nên \(\widehat{C_1}=\left(180+20\right):2=100^0\)
\(\widehat{C_2}=180-100=80^0\)
mà \(\widehat{C_1}+\widehat{D_1}=180^0\)
→\(\widehat{D_1}=180-\widehat{C_1}=180-100\)
→\(\widehat{D_1}=80^0\)
mà \(\widehat{C_1}và\widehat{D_2}\) so le trong nên \(\widehat{D_2}=\widehat{C_1}=100^0\)