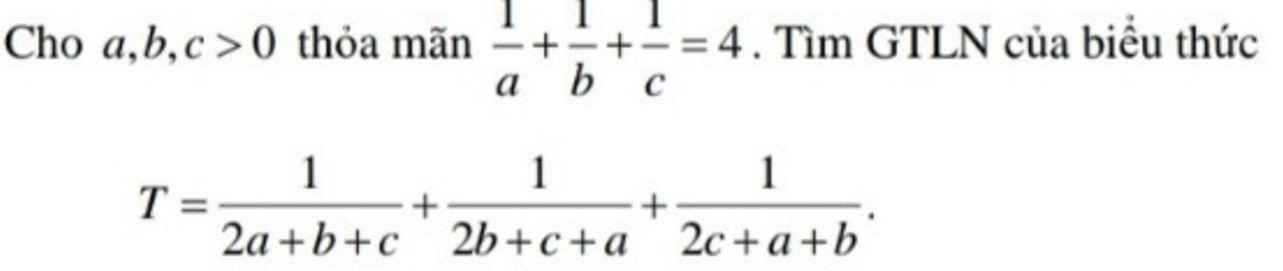\(đặt\left(\dfrac{1}{a};\dfrac{1}{b};\dfrac{1}{c}\right)=\left(x;y;z\right)\Leftrightarrow x+y+z=4\)
\(T=\Sigma\dfrac{1}{\dfrac{2}{x}+\dfrac{1}{y}+\dfrac{1}{z}}=\Sigma\dfrac{1}{\dfrac{1}{x}+\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}}\le\dfrac{1}{16}\left(x+x+y+z+y+y+x+z+z+z+x+y\right)=\dfrac{1}{16}4\left(x+y+z\right)=1\)
không đặt ẩn cũng được \(T=\dfrac{1}{2a+b+c}+\dfrac{1}{2b+c+a}+\dfrac{1}{2c+a+b}\)
\(\dfrac{1}{2a+b+c}\le\dfrac{1}{4}\left(\dfrac{1}{2a}+\dfrac{1}{b+c}\right)\le\dfrac{1}{4}\left(\dfrac{1}{2a}+\dfrac{1}{4b}+\dfrac{1}{4c}\right)\)
\(tương\) \(tự\Rightarrow T\le\dfrac{1}{4}\left(\dfrac{1}{2a}+\dfrac{1}{4b}+\dfrac{1}{4c}+\dfrac{1}{2b}+\dfrac{1}{4c}+\dfrac{1}{4a}+\dfrac{1}{2c}+\dfrac{1}{4a}+\dfrac{1}{4b}\right)=\dfrac{1}{4}\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{4}\right)=\dfrac{1}{4}.4=1\)
\(dấu"="\Leftrightarrow a=b=c=\dfrac{3}{4}\)