a) Ta có: góc xOy và góc yOz kề bù => góc xOy + góc yOz = 180 độ
<=> góc yOz = 180 độ - 120 độ = 60 độ
b) Ta có : Ot là tia phân giác của xOy
=> góc yOt = góc xOy/2= 120/2 = 60 độ
Ta có: góc zOt= góc yOt + góc yOz
<=> góc zOt= 60 độ + 60 độ = 120 độ
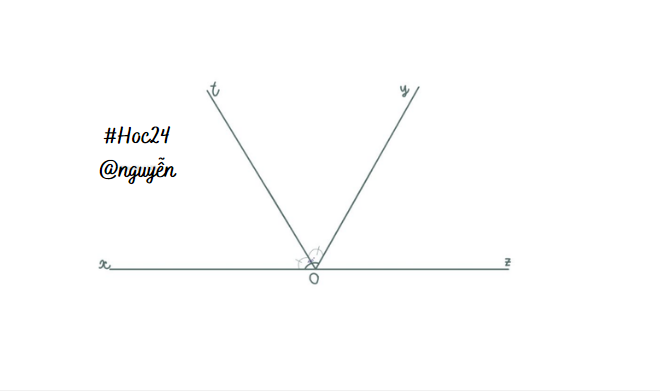
`a)` Ta có : \(\widehat{xOy}kề.bù\left(yOz\right)\left(gt\right)\)
\(\Rightarrow\widehat{xOy}+\widehat{yOz}=180^0\)
\(\Rightarrow\widehat{yOz}=180^0-\widehat{xOy}\)
`=180^0 - 120^0`
`=60^0`
Vậy \(\widehat{yOz}=60^0\)
`b)` Vì `Ot` là tia phân giác của \(\widehat{xOy}\left(gt\right)\)
\(\Rightarrow\widehat{yOt}=\dfrac{\widehat{xOy}}{2}=\dfrac{120^0}{2}=60^0\)
Ta có: \(\widehat{zOt}=\widehat{yOz}+\widehat{yOt}\)
`=60^0 + 60^0`
`=120^0`
Vậy \(\widehat{zOt}=120^0\)
`c)` Trên nửa mặt phẳng bờ `xz` có \(\widehat{zOy}< \widehat{zOt}\left(60^0< 120^0\right)\)
`=>Oy` nằm giữa hai tia `Oz` và `Ot`
Lại có \(\widehat{zOy}=\widehat{yOt}=60^0=\dfrac{120^0}{2}=\dfrac{\widehat{zOt}}{2}\)
`=>Oy` là tia phân giác của \(\widehat{zOt}\)
hình ko đo nên có thể sai
a/ vì xOy và yOz kề bù nên
xOy+yOz=180
→yOz=180-xOy=180-120
→yOz=60 độ
b/
vì Ot là tia phân giác của xOy
xOt=tOy=xOy/2=120/2=60
mà zOt=tOy+tOz
→zOt=60+60
→zOt=120
c/
ta có zOy<zOt(60<120) nên Oy nằm giữa Ot và Oz
mà zOy=zOt=60 độ
suy ra Oy là phân giác của zOt






