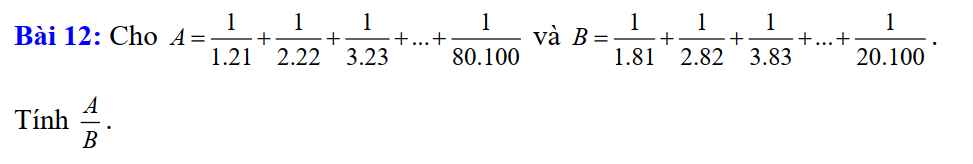Question

Answer 1

À dạ mời bn tham khảo:

Ta có `:A=1/1.21 + 1/2.22 + 1/3.23 + ...+ 1/80.100`

`20A=20/1.21+20/2.22+20/3.23+...+20/80.100`

`20A=1/1-1/21+1/2-1/22+1/3-1/23+...+1/80-1/100`

`20A=(1+1/2+1/3+...+1/80)-(1/21+1/22+1/23+...+1/100)`

Có `:B=1/1.81+1/2.82+1/3.83+...+1/20.100`

`80B=80/1.81+80/1.82+....+80/20.100`

`80B=1/1-1/81+1/2-1/82+...+1/20-1/100`

`80B=(1+1/2+...+1/20)-(1/81+1/82+...+1/100)`

`80B=(1+1/2+...+1/20+1/21+1/22+...+1/80)-(1/21+1/22+...+1/80+1/81+1/82+...+1/100)`

`80B=(1+1/2+...+1/80)-(1/21+1/22+...+1/100)`

`(20A)/(80B)=( (1+1/2+...+1/80)-(1/21+1/22+...+1/100) )/( (1+1/2+...+1/80)-(1/21+1/22+...+1/100) )`

`(20A)/(80B)=1`

`20A=80B`

`A/B=80/20=4`

Vậy `A/B=1/4`

Answer 2

Em coi bài chị lm bên hoidap nha :333